Online Calculators since 2009

Popular Today

Physics 2D Vector Calculator

The 2D Vector Calculator is an online physics calculator provided in support of our Physics Tutorial on Vectors and Scalars. On this page you will find an online Vector Calculator, instructions on how to calculate vectors and how to use the vector calculator, links to additional vector calculators and supporting information. This Vector Calculator includes an example image to illustrate the inputs, precise results and detailed, step-by-step calculations of vectors so that you can gain a clear understanding of manual vector calculations and check your own vector calculations for accuracy when studying Vectors in Physics.

This vector calculator is used for two purposes:

To calculate the components of a vector quantity in Physics when the original vector and the angle it forms with the horizontal direction are given, and
To calculate the vector's magnitude, angle with the horizontal direction and also the cosine, sine, cotangent and tangent of this angle.

The Vector Calculator already contains sample values, these are based on the Physics Tutorial on Vectors and Scalars. Simply enter your own units of measurement to produce a new vector calculation.

2D Vector Calculator
🖹 Normal View🗖 Full Page View
Show Vector ImageHide Vector Image
Calculate
AB_x (Newton, N)
AB_y (Newton, N)

2D Vector Calculator Calculations and Results
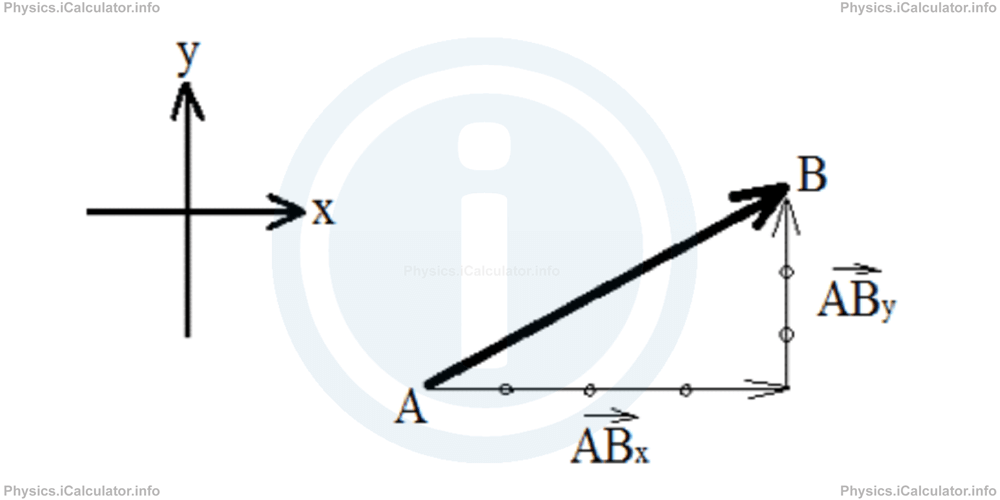Results [see further down for step by step calculations]
Magnitude of the vector \|AB⃗\| is
cos θ is °
sin θ is °
cot θ is °
tan θ is °
Magnitude of Force Calculation
\|AB⃗\| = √AB²_x + AB²_y \|AB⃗\| = √² +² \|AB⃗\| = √ + \|AB⃗\| = √ \|AB⃗\| =
cos θ Calculation
cos θ = **Adjacent side/Hypotenuse = AB_x/\|AB⃗\|** cos θ = / cos θ =
sin θ Calculation
sin θ = **Opposite side/Hypotenuse = AB_y/\|AB⃗\|** sin θ = / sin θ =
cot θ Calculation
cot θ = **Adjacent side/Opposite side = AB_x/AB_y** cot θ = / cot θ =
tan θ Calculation
tan θ = **Opposite side/Adjacent side = AB_y/AB_x** tan θ = / tan θ =

★★★★★ [ 12 Votes ]

Units of Measurement used within the Physics Vector Calculator

Vectors Measurements and Units
Measurement	Units
Force, F	Newton, N
Displacement, Δr	Metre, m
Velocity, v	Metre per second, m/s
Acceleration, a	Metre per square second, m/s2
Electric field. E	Volt per metre, V/m
Magnetic induction, B	Tesla, T
Linear momentum, p	Kilogram metre per second, kg ∙ m/s

tip! It is good to know that all physical quantities are either scalars or vectors. A vector quantity in Physics is considered as known if three clues are provided:

Magnitude
Direction
Unit
Application point

If one of the above elements is missing, the info about the vector quantity in question is incomplete.

Usually, a vector forms an angle Θ to the horizontal direction.

For an easier understanding, a vector quantity A⃗ can be projected on the main axes.

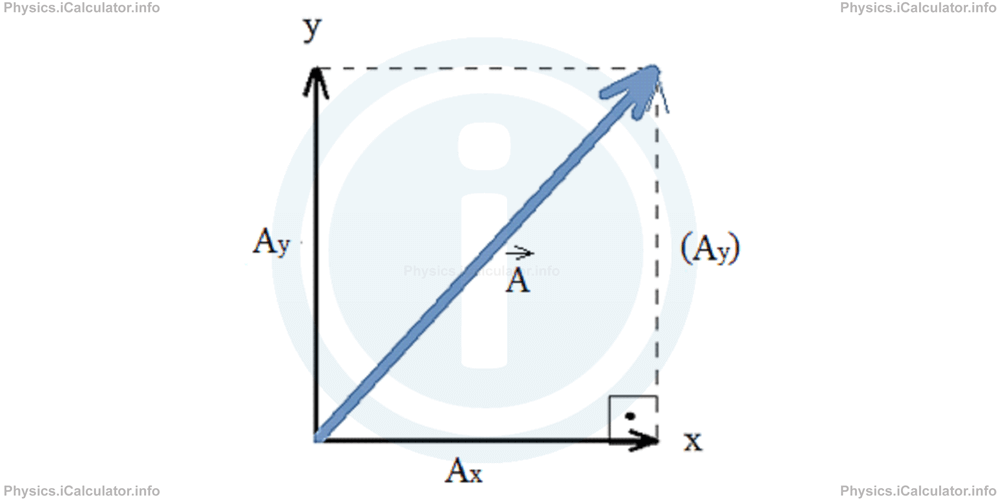
The equations used for the vector projections (components) are:

A_x = |A⃗| × cos Θ
A_y = |A⃗| × sin Θ
|A⃗| = √A²_x + A²_y
cot Θ = A_x/A_y
cot Θ = A_y/A_x

In Physics, the vector A⃗ may represent many quantities. Some of them include:

Force F, Displacement Δr, Velocity v, Acceleration, a, Electric field E, Magnetic induction B, Linear momentum p and many others but only these are included in the calculator.

How the Vector Calculator works?

When you choose one of the above quantities (generally denoted by A⃗ but the actual symbol fits the specific quantity chosen), you can insert the magnitude and the angle Θ to the horizontal direction. Then the calculator gives the values of vector components A_x and A_y.

On the other hand, if you insert the components A_x and A_y, the calculator provides the following values:

The vector magnitude
The angle Θ between the vector and the horizontal direction
The cosine of the angle formed by the vector and the horizontal direction
The sine of the angle formed by the vector and the horizontal direction
The cotangent of the angle formed by the vector and the horizontal direction
The tangent of the angle formed by the vector and the horizontal direction

Therefore, it is a very useful tool to be used in the 2-D analysis of the most important physical vector quantities included in General Physics.

Related Vector Calculators by iCalculator

Physics Calculators

You may also find the following Physics calculators useful.