Menu
Physics Lesson 6.2.4 - Centre of Mass of Three non-Collinear Objects
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Centre of Mass of Three non-Collinear Objects, this is the fourth lesson of our suite of physics lessons covering the topic of Determining the Centre of Mass in Objects and Systems of Objects, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Centre of Mass of Three non-Collinear Objects
In this case, we must consider a triangle in which objects' centres of gravity act as vertices as shown in the figure. 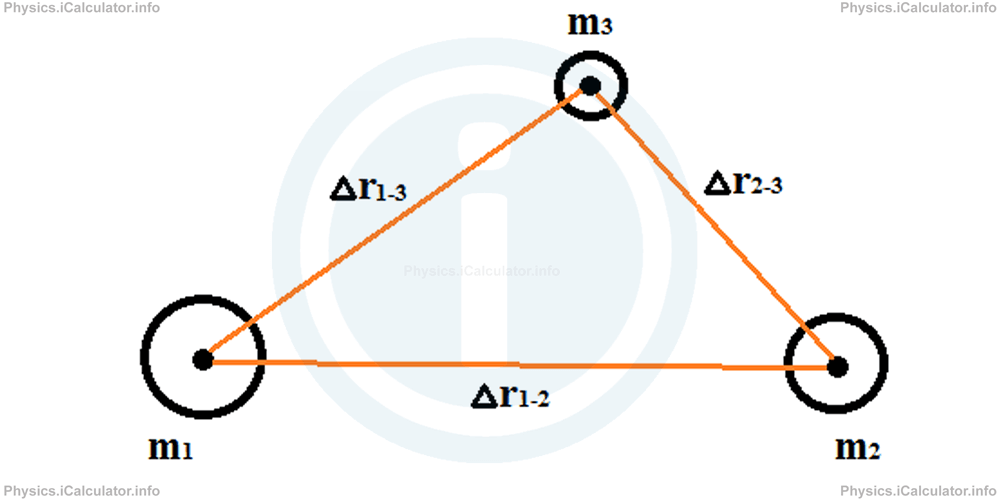
Again, we think the sides of this triangle as very light sticks with negligible weight. They are drawn in the figure only for calculation purpose. Also, we can think the inner part of the triangle as made by a very thin and light layer, such as a transparent vinyl sheet or anything similar.
It is obvious that the centre of gravity of the system is somewhere inside the internal area of triangle. It acts as an equilibrium point of the system, i.e. if we put the system on a pivot, which is exactly below the centre of mass, it stays in equilibrium as shown below. 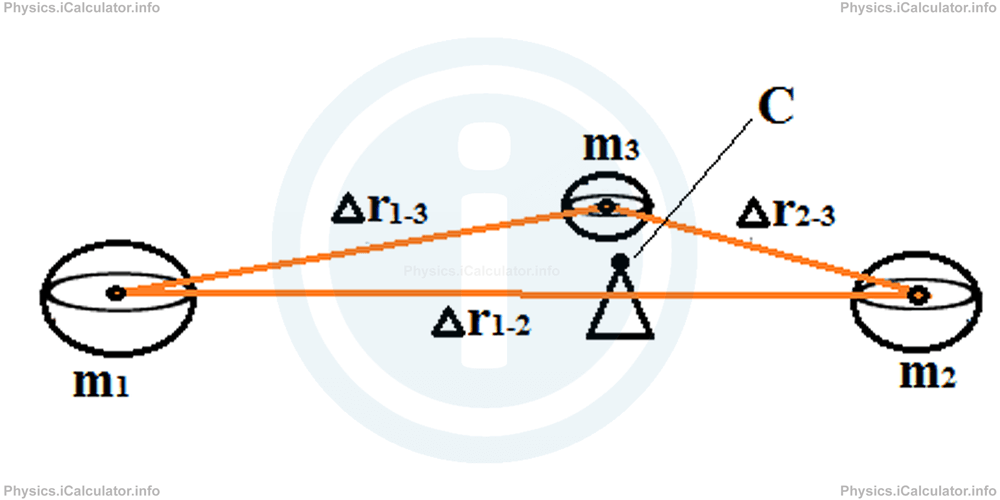
We must consider two dimensions in order to work out the centre of mass if the system. Therefore, the equation (1) is applied for both x and y coordinates. This means the centre of mass of the system is written in the format (xC, yC). Hence, we write
and
A comprehensive approach in this regard involves dealing with some mathematical concepts such as the equation of a line that passes through two known points, the angles of a triangle when the side lengths are known, etc. These concepts are not difficult; a student learns all them in high school math. However, dealing with such concepts goes beyond the scope of this tutorial. Here we will discuss only situations involving objects whose centre of mass have known coordinates, so that we can apply directly the equation (1) for two dimensions.
Let's illustrate this point through an example.
Example 4
Three objects are connected with very light sticks to form a single system. The first object has a mass of 4 kg and it is at (0m, 3m). The second object has a mass of 1 kg and it is at (-1m, 0m), and the third object has a mass of 2 kg and it is at (5m, 4m). Where is the centre of mass of the system?
Solution 4
In this example, it is better to draw a coordinate system and show all objects visually.
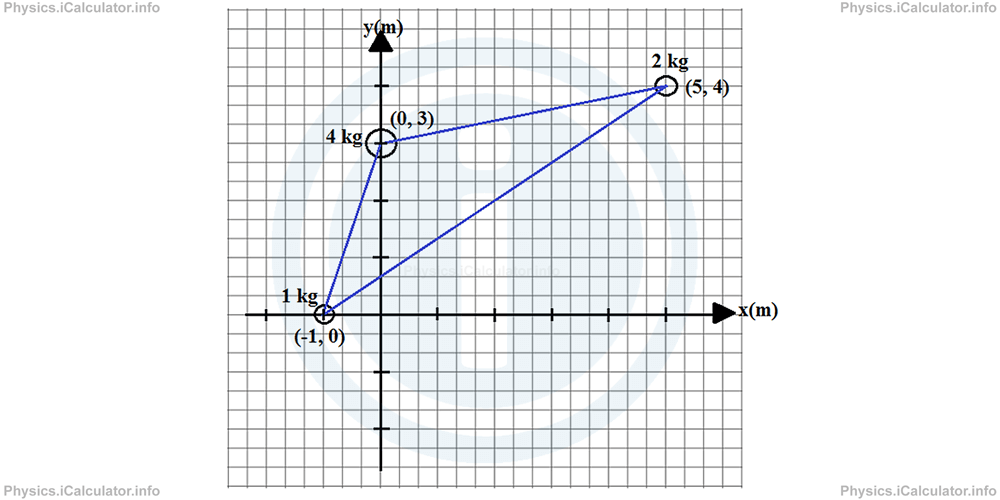
Now, let's write the clues. We have:
m2 = 1 kg
m3 = 2 kg
x1 = 0 m
x2 = -1 m
x3 = 5 m
y1 = 3 m
y2 = 0 m
y3 = 4 m
xC = ?
yC = ?
Applying the equation (1) for the x and y-direction separately, we obtain
= 0 × 4 + (-1) × 1 + 5 × 2/4 + 1 + 2
= -1 + 10/7
= 9/7 m
≈ 1.29 m
and
= 3 × 4 + 0 × 1 + 4 × 2/4 + 1 + 2
= 12 + 8/7
= 20/7
≈ 2.86 m
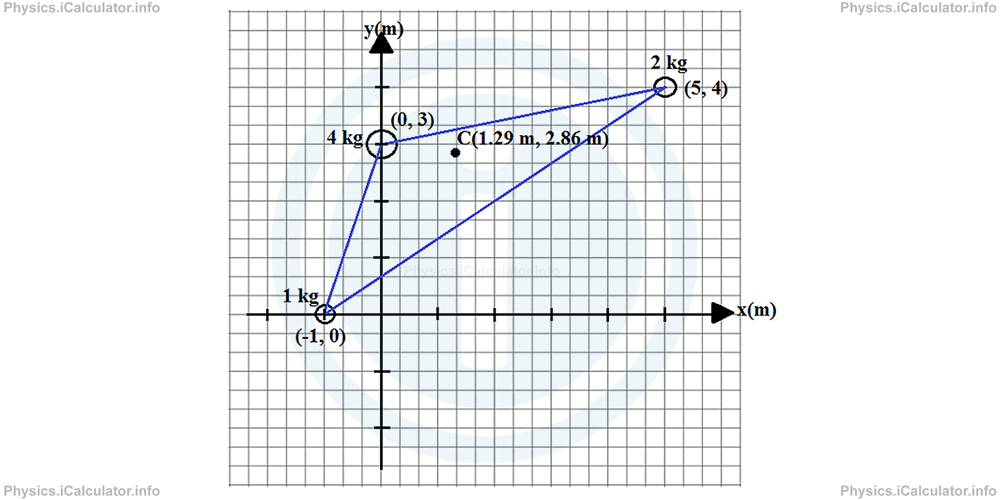
Therefore, the centre of gravity of the system is at (1.29 m, 2.86 m). Look at the figure:
Even for three dimensions, we use the same method. The only difference is that we have another dimension, the z-dimension. Therefore, we must apply three times the equation (1).
You have reached the end of Physics lesson 6.2.4 Centre of Mass of Three non-Collinear Objects. There are 4 lessons in this physics tutorial covering Determining the Centre of Mass in Objects and Systems of Objects, you can access all the lessons from this tutorial below.
More Determining the Centre of Mass in Objects and Systems of Objects Lessons and Learning Resources
Whats next?
Enjoy the "Centre of Mass of Three non-Collinear Objects" physics lesson? People who liked the "Determining the Centre of Mass in Objects and Systems of Objects lesson found the following resources useful:
- Non Collinear Feedback. Helps other - Leave a rating for this non collinear (see below)
- Centre of Mass and Linear Momentum Physics tutorial: Determining the Centre of Mass in Objects and Systems of Objects. Read the Determining the Centre of Mass in Objects and Systems of Objects physics tutorial and build your physics knowledge of Centre of Mass and Linear Momentum
- Centre of Mass and Linear Momentum Revision Notes: Determining the Centre of Mass in Objects and Systems of Objects. Print the notes so you can revise the key points covered in the physics tutorial for Determining the Centre of Mass in Objects and Systems of Objects
- Centre of Mass and Linear Momentum Practice Questions: Determining the Centre of Mass in Objects and Systems of Objects. Test and improve your knowledge of Determining the Centre of Mass in Objects and Systems of Objects with example questins and answers
- Check your calculations for Centre of Mass and Linear Momentum questions with our excellent Centre of Mass and Linear Momentum calculators which contain full equations and calculations clearly displayed line by line. See the Centre of Mass and Linear Momentum Calculators by iCalculator™ below.
- Continuing learning centre of mass and linear momentum - read our next physics tutorial: Newton's Second Law for System of Particles
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Determining the Centre of Mass in Objects and Systems of Objects" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.