Menu
Physics Lesson 6.2.1 - Centre of Mass of a Regular Non-Homogenous Object
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Centre of Mass of a Regular Non-Homogenous Object, this is the first lesson of our suite of physics lessons covering the topic of Determining the Centre of Mass in Objects and Systems of Objects, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Centre of Mass of a Regular Non-Homogenous Object
The simplest example of a regular non-homogenous object is a long and thin bar composed by two different materials, which are attached longwise as shown below.
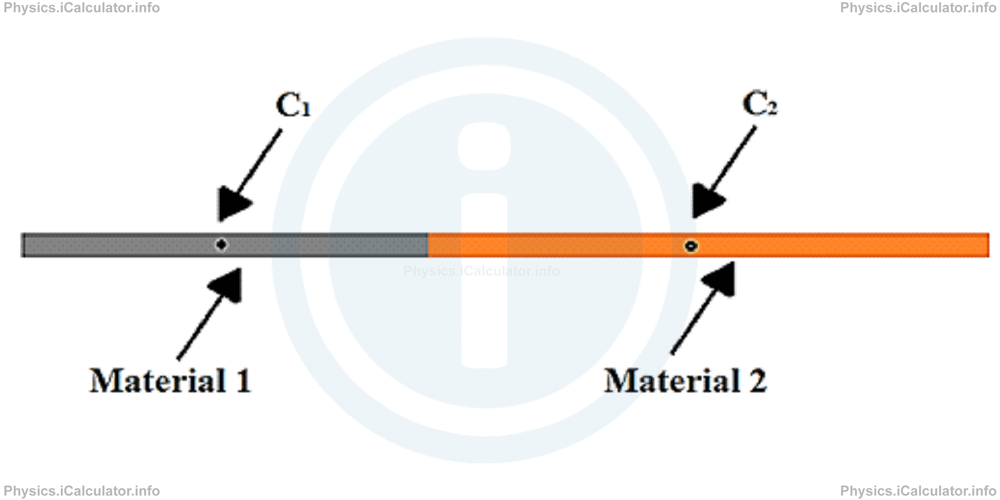
Each individual bar has its own centre of mass if taken separately. These centres of mass are denoted by C1 and C2 respectively. Since the bars are both homogenous and regularly shaped (they are either prisms or cylinders, depending on their base shape), the centre of gravity for each bar is located at middle of their respective length.
First of all, we must choose a reference point or origin (as discussed in the Kinematics section). For convenience, we can chose the origin at the left-end of the first bar, which corresponds to the left-end of the entire system. Since the bars are very thin, we need only the x-dimension for calculating the centre of mass of the whole system. Therefore, we can write as x1 and x2 the values for the x-coordinates of each individual centre of mass. For example, if the lengths of each individual bar are L1 and L2 respectively, we have for the coordinates of their centre of gravity,
and
Look at the figure below to create a clearer idea in this regard.
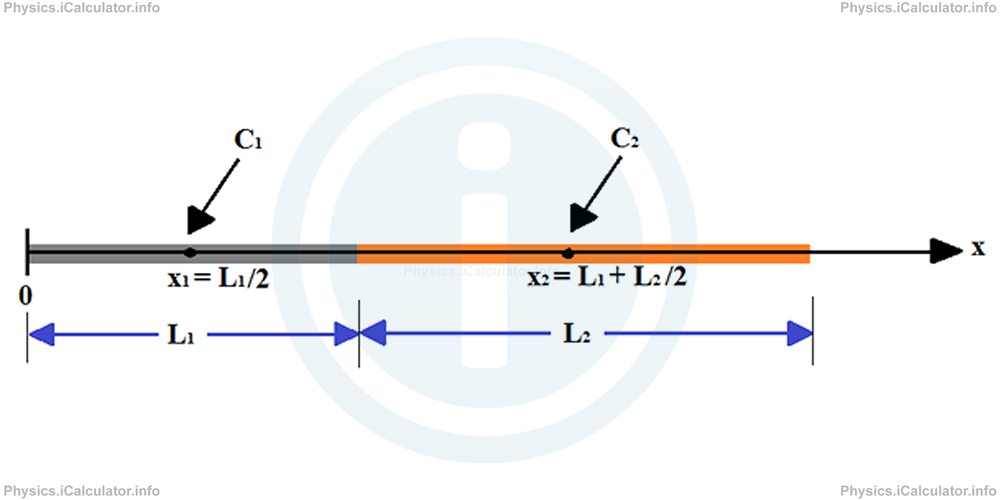
To determine the centre of mass C of the system, we must also consider the masses of each individual bar (since they are made from different materials, we don't expect to have equal masses although the lengths may be equal). Thus, if m1 and m2 are the masses of each individual bar respectively, the centre of mass xC of this system is calculated by the formula
Equation 1
xC = x1 × m1 + x2 × m2/m1 + m2The above Equation is widely used in other field of science as well. You may encounter it (only as a structure but with different quantities obviously) in mathematics, finance, etc. This Equation can be extended for more than two materials as well.
Example 1
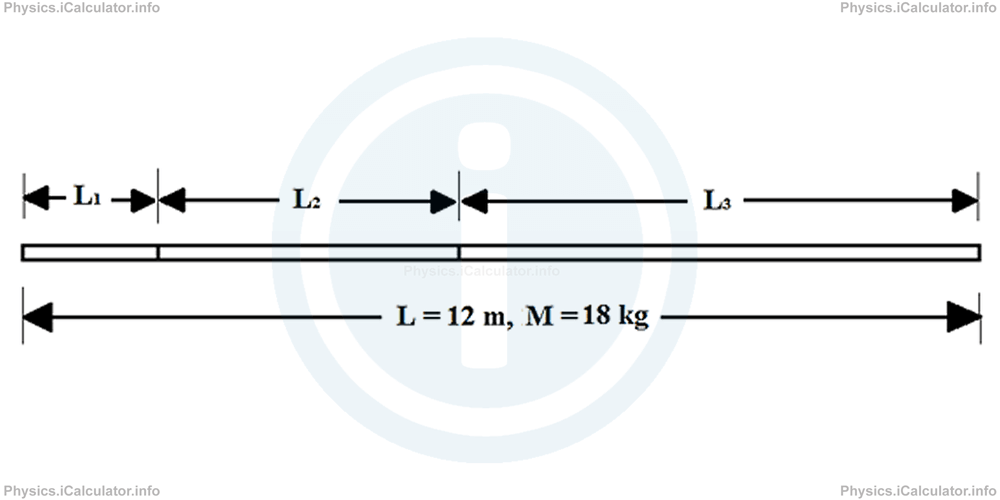
A long and thin bar is made from three different materials. The total length of the bar is 12 m and the ratio of its pieces in respect to length is L1 : L2 : L3 = 1 : 2 : 3. Also, the total mass of the bar is 18 kg and the ratio of pieces in respect to mass is m1 : m2 : m3 = 3 : 2 : 4.
If the order from left to right is 1 - 2 - 3, calculate the centre of gravity from the left end of the bar.
Solution 1
First, we must draw a figure to have a better idea on the situation described in this problem.
Now, let's determine the values for lengths and masses of each piece.
We have:
Also (as a ratio),
Hence, we can write
L1 = 1 × x, L2 = 2 × x and L3 = 3 × x
Therefore,
6 × x = 12 m
x = 2m
Thus,
L2 = 2 × 2m = 4m
L3 = 3 × 2m = 6m
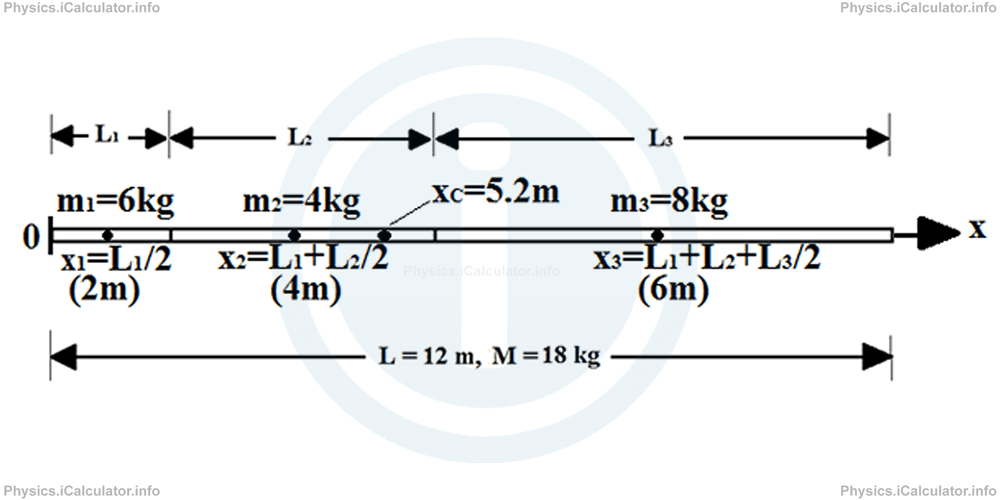
Thus, for the x-coordinates of each centre of mass, we have
x2 = L1 + L2/2 = 2m + 4m/2 = 4m
x3 = L1 + L2 + L3/2 = 2m + 4m + 6m/2 = 9m
The same procedure is used to calculate the masses of each piece. We have
Also,
Hence, we can write
m1 = 3 × x, m2 = 2 × x and m3 = 4 × x
Therefore,
9 × x = 18 kg
x = 2 kg
Thus,
m2 = 2 × 2 kg = 4 kg
m3 = 4 × 2 m = 8 kg
Now, let's use the equation (1) to calculate the centre of mass of this system. We have:
= 1 × 6 + 4 × 4 + 9 × 8/6 + 4 + 8
= 94/18 m
≈ 5.2 m
This means the centre of gravity of this system is at the second bar, 0.8 m on the left of its end (or the beginning of the third bar), as shown in the figure below.
What does this result mean?
The result obtained means that if we hang or put the object on a pivot, it will stay in equilibrium only if the string or the pivot are at 5.2 m from the left side of the composite bar. If we hang or put it at whatever point other than xC = 5.2 m, it will lean aside. Look at the figures below:
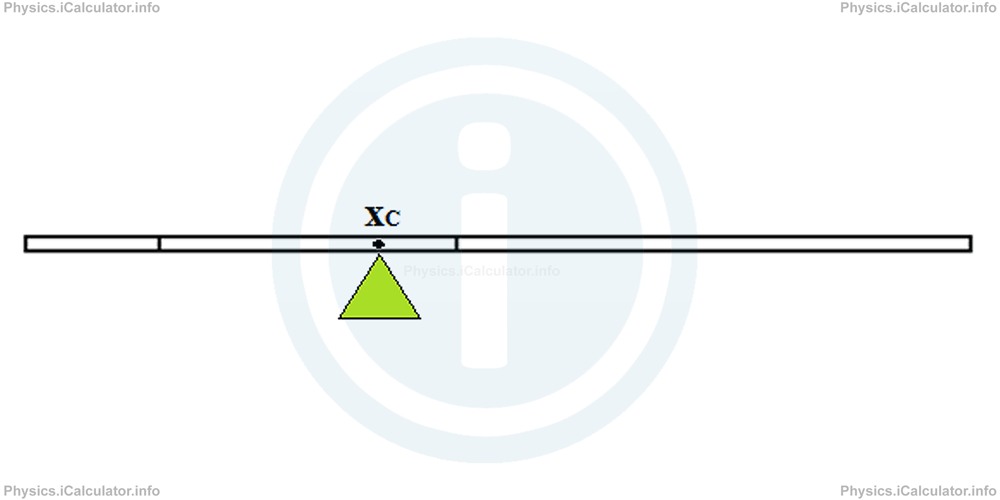
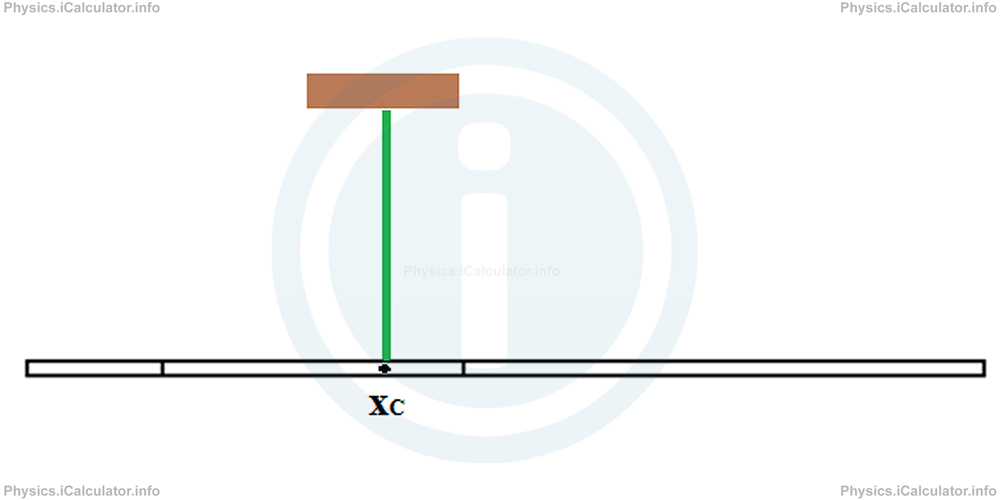
You have reached the end of Physics lesson 6.2.1 Centre of Mass of a Regular Non-Homogenous Object. There are 4 lessons in this physics tutorial covering Determining the Centre of Mass in Objects and Systems of Objects, you can access all the lessons from this tutorial below.
More Determining the Centre of Mass in Objects and Systems of Objects Lessons and Learning Resources
Whats next?
Enjoy the "Centre of Mass of a Regular Non-Homogenous Object" physics lesson? People who liked the "Determining the Centre of Mass in Objects and Systems of Objects lesson found the following resources useful:
- Non Homogenous Feedback. Helps other - Leave a rating for this non homogenous (see below)
- Centre of Mass and Linear Momentum Physics tutorial: Determining the Centre of Mass in Objects and Systems of Objects. Read the Determining the Centre of Mass in Objects and Systems of Objects physics tutorial and build your physics knowledge of Centre of Mass and Linear Momentum
- Centre of Mass and Linear Momentum Revision Notes: Determining the Centre of Mass in Objects and Systems of Objects. Print the notes so you can revise the key points covered in the physics tutorial for Determining the Centre of Mass in Objects and Systems of Objects
- Centre of Mass and Linear Momentum Practice Questions: Determining the Centre of Mass in Objects and Systems of Objects. Test and improve your knowledge of Determining the Centre of Mass in Objects and Systems of Objects with example questins and answers
- Check your calculations for Centre of Mass and Linear Momentum questions with our excellent Centre of Mass and Linear Momentum calculators which contain full equations and calculations clearly displayed line by line. See the Centre of Mass and Linear Momentum Calculators by iCalculator™ below.
- Continuing learning centre of mass and linear momentum - read our next physics tutorial: Newton's Second Law for System of Particles
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Determining the Centre of Mass in Objects and Systems of Objects" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.