Menu
Physics Lesson 6.2.2 - Centre of Mass of a System Composed by Two or More Distant Objects
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Centre of Mass of a System Composed by Two or More Distant Objects, this is the second lesson of our suite of physics lessons covering the topic of Determining the Centre of Mass in Objects and Systems of Objects, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Centre of Mass of a System Composed by Two or More Distant Objects
If there is a system composed by two or more objects, which have a certain distance between them, we can use a similar procedure to the one described in the previous paragraph for calculating its centre of mass if masses and positions (coordinates) of each object are known. Even when the objects are irregularly shaped, we can ignore their shape and concentrate only on their respective centres of mass.
Despite the objects are distant, we consider them as a single system of objects connected through very light sticks whose masses are neglected.
In the following example, we will show that it is not important where you take the origin when calculating the centre of mass of a system of objects as long as you make the calculations correctly.
Example 2
Two objects A and B of masses 4 kg and 2 kg respectively, are 6 m away from each other. Calculate the centre of gravity of the system.
Solution 2
We will take two different points of reference to show that this is not relevant in determining the centre of gravity of the system.
1. Let's take the reference point 1 m on the left of the first object as shown in the figure.
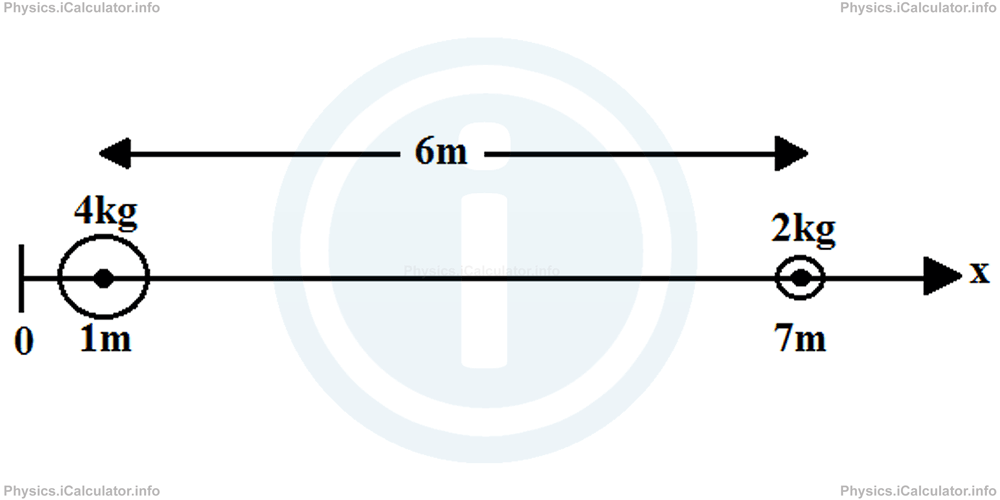
The clues for this configuration are:
x2 = 1 m + 6 m = 7 m
m1 = 4 kg
m2 = 2 kg
xC = ?
= 1 × 4 + 7 × 2/4 + 2
= 18/6 m
= 3 m
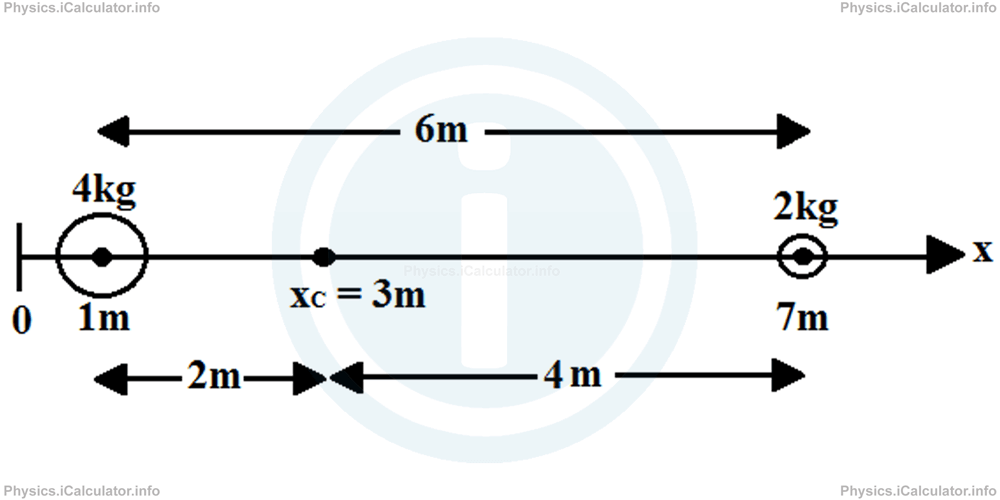
This result means the centre of gravity of the system is 2m on the right of the first object (3m - 1m = 2m) and 4m on the left of the second object (7m - 3m = 4m). Look at the figure:
2. If we take the origin at another position, for example 4m on the left of the first object, we obtain the following figure:
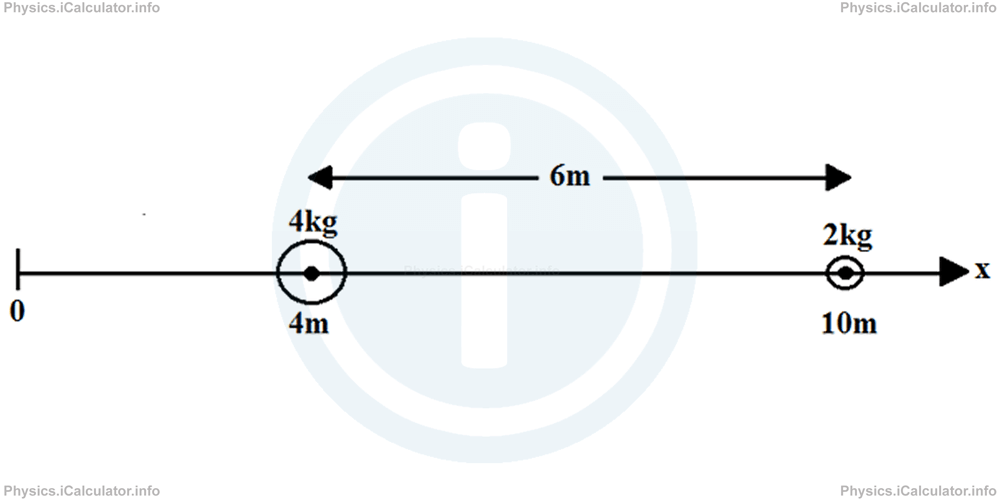
The clues for this new configuration are:
x2 = 4 m + 6 m = 10 m
m1 = 4 kg
m2 = 2 kg
xC = ?
Applying again the equation (1) we obtain
= 4 × 4 + 10 × 2/4 + 2
= 36/6 m
= 6 m
This result means the centre of gravity of the system is again 2m on the right of the first object (6m - 4m = 2m) and 4m on the left of the second object (10m - 6m = 4m). Look at the figure:
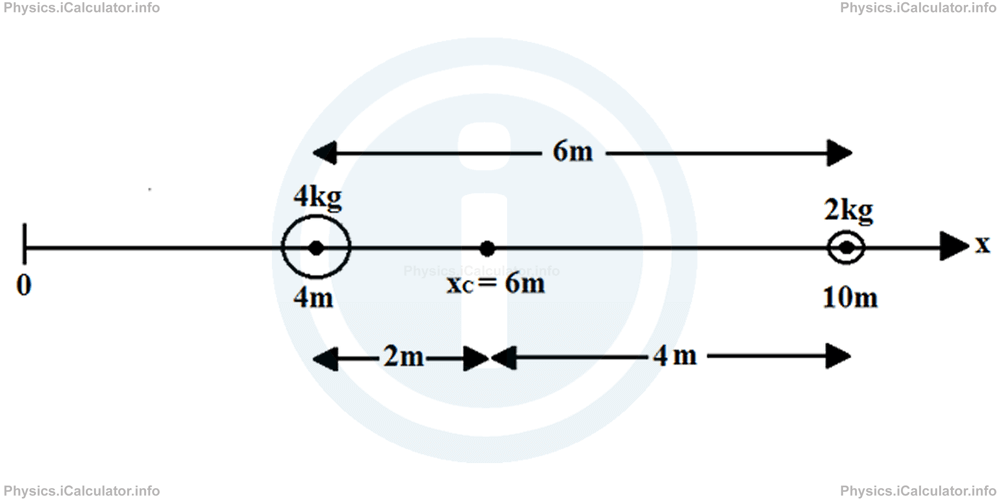
Therefore, we get the same result, no matter where we choose to take the reference point (origin).
You have reached the end of Physics lesson 6.2.2 Centre of Mass of a System Composed by Two or More Distant Objects. There are 4 lessons in this physics tutorial covering Determining the Centre of Mass in Objects and Systems of Objects, you can access all the lessons from this tutorial below.
More Determining the Centre of Mass in Objects and Systems of Objects Lessons and Learning Resources
Whats next?
Enjoy the "Centre of Mass of a System Composed by Two or More Distant Objects" physics lesson? People who liked the "Determining the Centre of Mass in Objects and Systems of Objects lesson found the following resources useful:
- System Composed Feedback. Helps other - Leave a rating for this system composed (see below)
- Centre of Mass and Linear Momentum Physics tutorial: Determining the Centre of Mass in Objects and Systems of Objects. Read the Determining the Centre of Mass in Objects and Systems of Objects physics tutorial and build your physics knowledge of Centre of Mass and Linear Momentum
- Centre of Mass and Linear Momentum Revision Notes: Determining the Centre of Mass in Objects and Systems of Objects. Print the notes so you can revise the key points covered in the physics tutorial for Determining the Centre of Mass in Objects and Systems of Objects
- Centre of Mass and Linear Momentum Practice Questions: Determining the Centre of Mass in Objects and Systems of Objects. Test and improve your knowledge of Determining the Centre of Mass in Objects and Systems of Objects with example questins and answers
- Check your calculations for Centre of Mass and Linear Momentum questions with our excellent Centre of Mass and Linear Momentum calculators which contain full equations and calculations clearly displayed line by line. See the Centre of Mass and Linear Momentum Calculators by iCalculator™ below.
- Continuing learning centre of mass and linear momentum - read our next physics tutorial: Newton's Second Law for System of Particles
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Determining the Centre of Mass in Objects and Systems of Objects" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.