Physics Tutorial 6.5 - Linear Momentum

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 2 Votes ]

There are 2 lessons in this physics tutorial covering Linear Momentum. The tutorial starts with an introduction to Linear Momentum and is then followed with a list of the separate lessons, the tutorial is designed to be read in order but you can skip to a specific lesson or return to recover a specific physics lesson as required to build your physics knowledge of Linear Momentum. you can access all the lessons from this tutorial below.

In this Physics tutorial, you will learn:

The definition of linear momentum
How to find linear momentum of a moving object
What does linear momentum represent?
Where does the linear momentum differ from the moment of force?

Introduction

Suppose you throw horizontally a tennis ball towards a wall. It is obvious the tennis ball will turn back after hitting the wall. We don't expect it turn back at the same speed because it loses some kinetic energy during the collision - energy which turns into other forms such as heat, sound energy etc. Therefore, the speed after the collision may be slightly smaller than before hitting the wall.

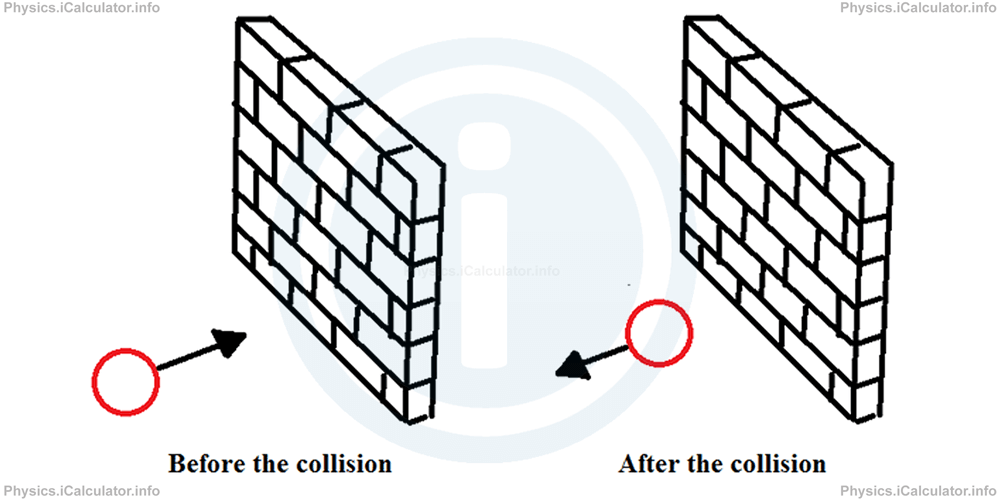
Physics Tutorials: This image provides visual information for the physics tutorial Linear Momentum

Now think about the same tennis ball hitting a very thin sheet of paper. It is obvious that the tennis ball will pierce the sheet and move at the same direction as before. Sure, the ball may encounter some small resistance from the sheet and as a result, its speed may be slightly smaller than before. Hence, we may obtain the same value for the speed as in the case when the tennis ball hits the hard wall and turns back.

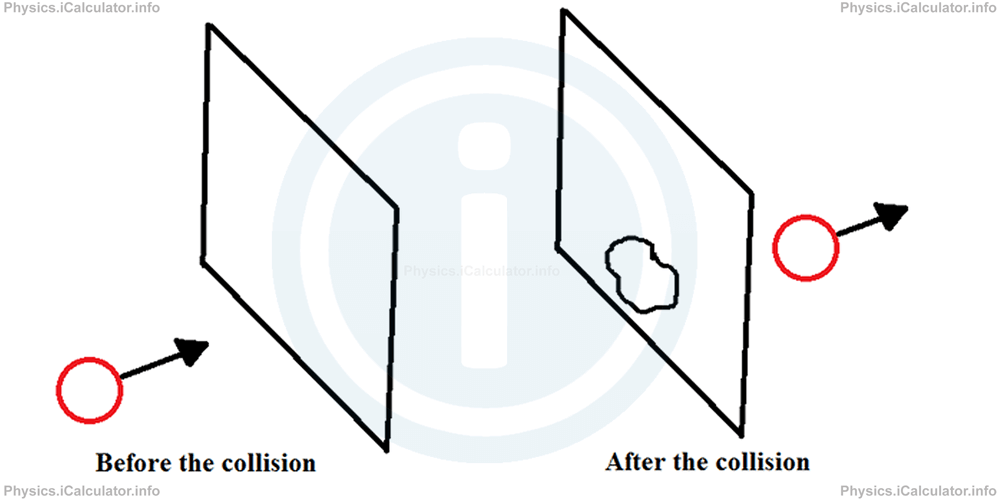
If we use the energetic approach, we get the same value for the initial and final kinetic energy in both cases, as energy is a scalar and as such, it doesn't involve any direction. Let's take some numbers only for illustration purpose. Thus, if we take the mass of the ball equal to 200 g (0.2 kg) and if the ball's initial speed in both cases is equal to 4 m/s and its final speed (in both cases again) is 3 m/s, we obtain for the initial kinetic energy in both cases,

KE_initial = m × v²_initial/2 = 0.2 × 4²/2 = 1.6 J

and for the final kinetic energy (in both cases),

KE_initial = m × v²_final/2 = 0.2 × 3²/2 = 0.9 J

Therefore, it would not make any difference whether the ball hits a wall or a sheet when dealing with mass and speed. We are only able to calculate the decrease in kinetic energy (1.6 J - 0.9 J = 0.7 J) which represents the amount of kinetic energy that has been converted into other forms during the collision.

Even if we used the respective velocities instead of speeds, the result would not change, as velocity is raised at power two in the formula of kinetic energy and therefore, we would obtain always a positive result, regardless the direction of velocity.

Thus, the energetic approach would be not so useful in making a thorough investigation of such events. If no figure or written information is provided, we are not able to detect whether the ball encounters a hard or a soft obstacle.

Hence, we need another approach, which besides the values of mass and velocity, consider the direction of motion as well. Such an approach, will be discussed and explained in the following paragraph.

Please select a specific "Linear Momentum" lesson from the table below, review the video tutorial, print the revision notes or use the practice question to improve your knowledge of this physics topic.

Centre of Mass and Linear Momentum Learning Material
Tutorial ID	Physics Tutorial Title	Revision Notes	Revision Questions
6.5	Linear Momentum
Lesson ID	Physics Lesson Title	Lesson	Video Lesson
6.5.1	Linear Momentum as a Quantity that Represents the Amount of Motion for an Object
6.5.2	Change in Momentum and its Importance in Understanding Objects' Motion

Whats next?

Enjoy the "Linear Momentum" physics tutorial? People who liked the "Linear Momentum" tutorial found the following resources useful:

Physics tutorial Feedback. Helps other - Leave a rating for this tutorial (see below)
Centre of Mass and Linear Momentum Revision Notes: Linear Momentum. Print the notes so you can revise the key points covered in the physics tutorial for Linear Momentum
Centre of Mass and Linear Momentum Practice Questions: Linear Momentum. Test and improve your knowledge of Linear Momentum with example questins and answers
Check your calculations for Centre of Mass and Linear Momentum questions with our excellent Centre of Mass and Linear Momentum calculators which contain full equations and calculations clearly displayed line by line. See the Centre of Mass and Linear Momentum Calculators by iCalculator™ below.
Continuing learning centre of mass and linear momentum - read our next physics tutorial: Collision and Impulse. Types of Collision

Centre of Mass and Linear Momentum Calculators

The following Physics Calculators are provided in support of the Centre of Mass and Linear Momentum tutorials.

Physics Calculators

You may also find the following Physics calculators useful.

Menu

Physics Tutorial 6.5 - Linear Momentum

Introduction

Whats next?

Centre of Mass and Linear Momentum Calculators

Physics Calculators