Physics Tutorial 6.3 - Newton's Second Law for System of Particles

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 7 Votes ]

There are 2 lessons in this physics tutorial covering Newton's Second Law for System of Particles. The tutorial starts with an introduction to Newton's Second Law for System of Particles and is then followed with a list of the separate lessons, the tutorial is designed to be read in order but you can skip to a specific lesson or return to recover a specific physics lesson as required to build your physics knowledge of Newton's Second Law for System of Particles. you can access all the lessons from this tutorial below.

In this Physics tutorial, you will learn:

The definition of particles in physics
The role of centre of mass in the dynamics of a system of particles
How to write the Newton's Second Law of Motion for a system of particles
How to make use of the help of coordinates to study the movement of a system of particles

Introduction

In the tutorial "Centre of Mass. Types of Equilibrium", we stated that centre of mass of an object helps us to determine its displacement, among other things. This is because an object may swing or rotate, besides moving linearly according a translational trajectory.

Consider a knife thrown towards a target table during a knife throwing activity. In many cases, the person involved holds the knife at its tip instead of its handle. After throwing the knife towards the table, it both rotates and displaces linearly. By the end of process, i.e. when it is stuck on the target table, the knife has rotated by a certain angle to its original direction because it spins several times during the flight.

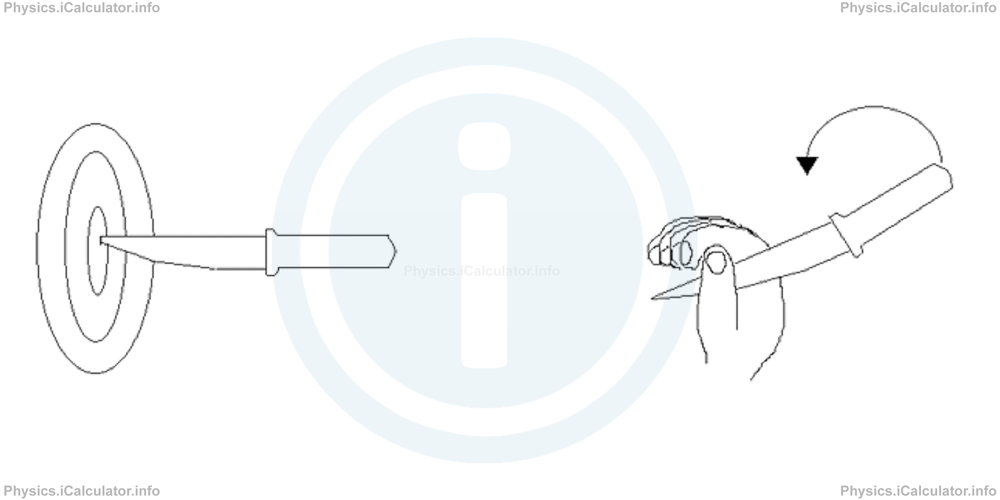
Physics Tutorials: This image provides visual information for the physics tutorial Newton's Second Law for System of Particles

For the above (and other) reasons, we cannot take the knife as a single object but as a system of points instead. It is obvious that the knife top travels a different distance from the handle. Of course, we can take the centre of mass as a representative of the object, but we know this is a generalization. However, when the object is too small in dimensions compared to the distance travelled by it, the study of the centre of mass is the only method available as if we try to study all points of the system, this would complicate a lot our task.

In this tutorial, we will deal with the motion of a system of particles by considering the forces acting in each individual particle. Obviously, we will deal only with two or three particles, as the method is the same for more particles as well. Increasing the number of particles only makes the calculations longer but the approach doesn't change.

Please select a specific "Newton's Second Law for System of Particles" lesson from the table below, review the video tutorial, print the revision notes or use the practice question to improve your knowledge of this physics topic.

Centre of Mass and Linear Momentum Learning Material
Tutorial ID	Physics Tutorial Title	Revision Notes	Revision Questions
6.3	Newton's Second Law for System of Particles
Lesson ID	Physics Lesson Title	Lesson	Video Lesson
6.3.1	Newton's Second Law for a System of Two Particles
6.3.2	Newton's Second Law of Motion for a System of Particles in Coordinates

Whats next?

Enjoy the "Newton's Second Law for System of Particles" physics tutorial? People who liked the "Newton's Second Law for System of Particles" tutorial found the following resources useful:

Physics tutorial Feedback. Helps other - Leave a rating for this tutorial (see below)
Centre of Mass and Linear Momentum Revision Notes: Newton's Second Law for System of Particles. Print the notes so you can revise the key points covered in the physics tutorial for Newton's Second Law for System of Particles
Centre of Mass and Linear Momentum Practice Questions: Newton's Second Law for System of Particles. Test and improve your knowledge of Newton's Second Law for System of Particles with example questins and answers
Check your calculations for Centre of Mass and Linear Momentum questions with our excellent Centre of Mass and Linear Momentum calculators which contain full equations and calculations clearly displayed line by line. See the Centre of Mass and Linear Momentum Calculators by iCalculator™ below.
Continuing learning centre of mass and linear momentum - read our next physics tutorial: Moment of Force. Conditions of Equilibrium

Centre of Mass and Linear Momentum Calculators

The following Physics Calculators are provided in support of the Centre of Mass and Linear Momentum tutorials.

Physics Calculators

You may also find the following Physics calculators useful.

Menu

Physics Tutorial 6.3 - Newton's Second Law for System of Particles

Introduction

Whats next?

Centre of Mass and Linear Momentum Calculators

Physics Calculators