Menu
Physics Lesson 6.3.1 - Newton's Second Law for a System of Two Particles
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Newton's Second Law for a System of Two Particles, this is the first lesson of our suite of physics lessons covering the topic of Newton's Second Law for System of Particles, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Newton's Second Law for a System of Two Particles
First, we must give the definition of particles in physics. Thus, "particles are objects whose dimensions are very small compared to their motion" Therefore, we do not consider the shape of particles at all during the calculation process and as a result, the study of their centre of mass gives the same result as the study of the entire system of particles.
Let's start with the simplest case - a system of two particles. Like in the previous tutorial, "Determining the Centre of Mass in Objects and Systems of Objects", we think them as connected by a very light stick whose mass is neglected. Look at the figure below.
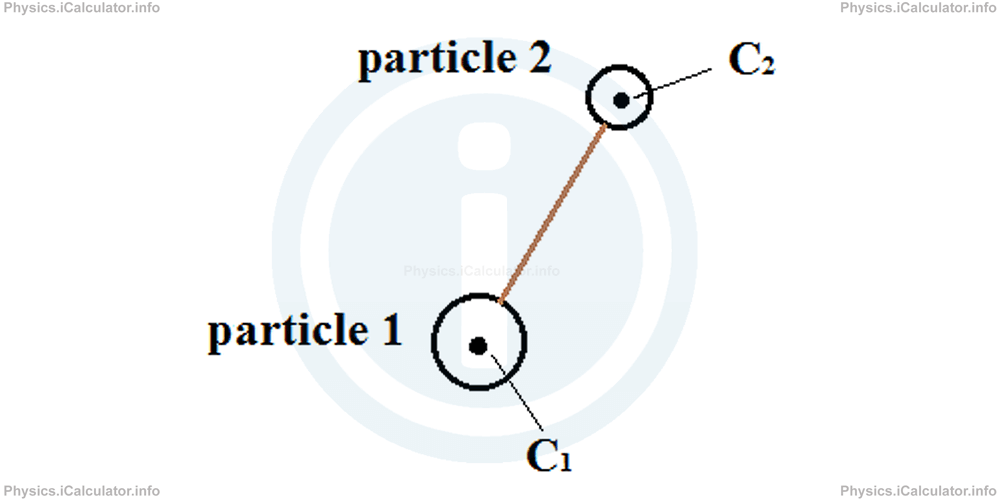
Let's suppose the system moves at another position in t seconds. As a result, we obtain this figure.
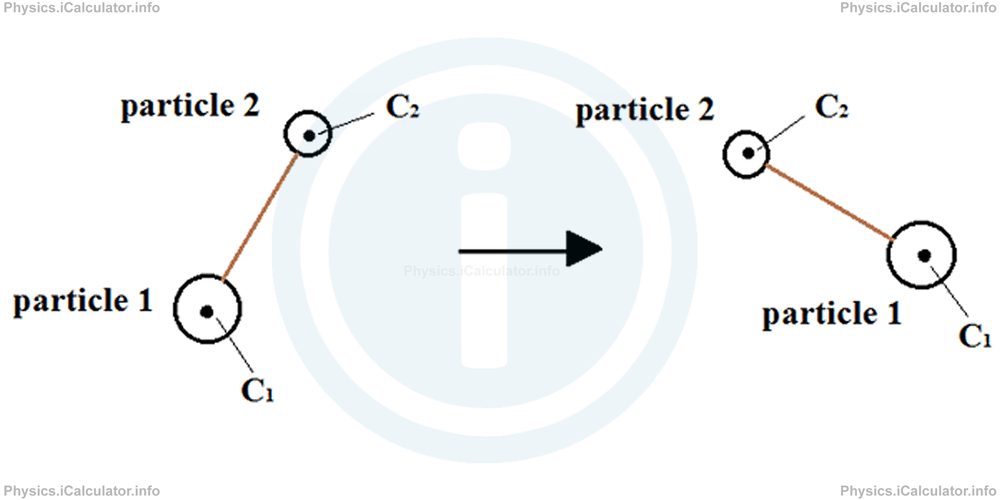
It is clear that the small particle (particle 2) is displaced less than the large one (particle 1). Therefore, either we must consider the objects as not related and thus calculating each displacement separately, or we must consider them as a single system and take an average value to represent the displacement just as we did in objects whose motion was irregular during the study of Kinematics.
Obviously, the second method is better, as it shortens the time of calculation and provides a good approximation of the values involved. For this, we need to consider again the centre of mass as a representative of the entire system and relate every kinematic or dynamic approach only to it.
Certainly, all objects move because of the action of any force. Therefore, if there is any motion of a certain object there is a force acting on the object as well. Thus, when a system moves, we can apply the Newton's Second law of Motion which - as discussed in the tutorial "Newton's Second Law of Motion" - outlines the relationship between acceleration, acting force and mass of an object.
The same thing can be said for a system of particles as well. We must only replace the mass of a single object by the mass of the entire system and the force acting on a single object (or better, the resultant force) with the resultant force acting on all particles of the system. Then, the equation
Equation 1
a⃗sys = F⃗R(sys)/msysis used to determine the acceleration of the entire system.
The extended Equation of the Newton's Second Law of Motion for a system of particles is
where 1, 2, 3, are the indexes for the objects included in the system.
Obviously, the equation (1) is in a vector form, so it is only a general expression of the Newton's Second law of Motion. We must write this equation in components, in order to make it applicable in practice. Therefore, we must write:
and
Then, we can use the Pythagorean Theorem to determine the magnitude of acceleration for this system of particles.
Equation 2
asys = √a2x(sys) + a2y(sys)Let's explain this point through an example.
Example 1
Two forces are acting in a system of particles as shown in the figure.
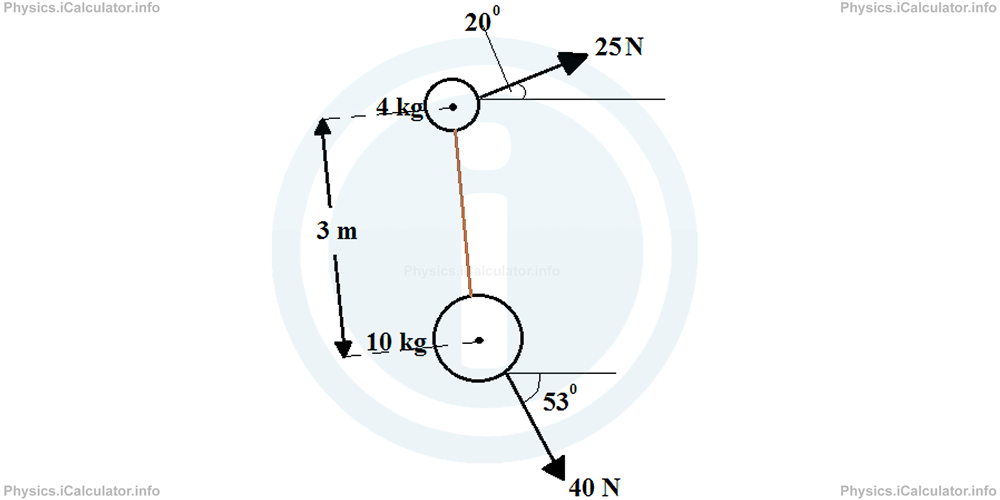
Forces act only at the initial stage, and then the system moves freely.
A light and non-stretchable bar connects the particles to each other. Their respective centres of mass are 3 m away. In the figure, you can also see the values for the masses and the acting force on the particles. The directions of forces and the angles they form to the horizontal direction are also given.
Calculate:
- The centre of mass of the system
- The initial acceleration of the system
Take cos 200 = 0.94, sin 200 = 0.34, cos 530 = 0.60 and sin 530 = 0.80.
Solution 1
a. Centre of mass of this system is determined by the equation
For simplicity, we can take the x-direction (only in this case) according the bar, which connects the two objects. Also we can take the origin at the centre of mass of any object, let's say at centre of the 10 kg object. As a result, we have the following clues:
x2 = 3 m
m1 = 10 kg
m2 = 4 kg
xC = ?
Substituting the above values, we obtain
= 12/14m
= 0.86 m
This result means the centre of gravity of this system is 0.86 m above the lower object as shown below:
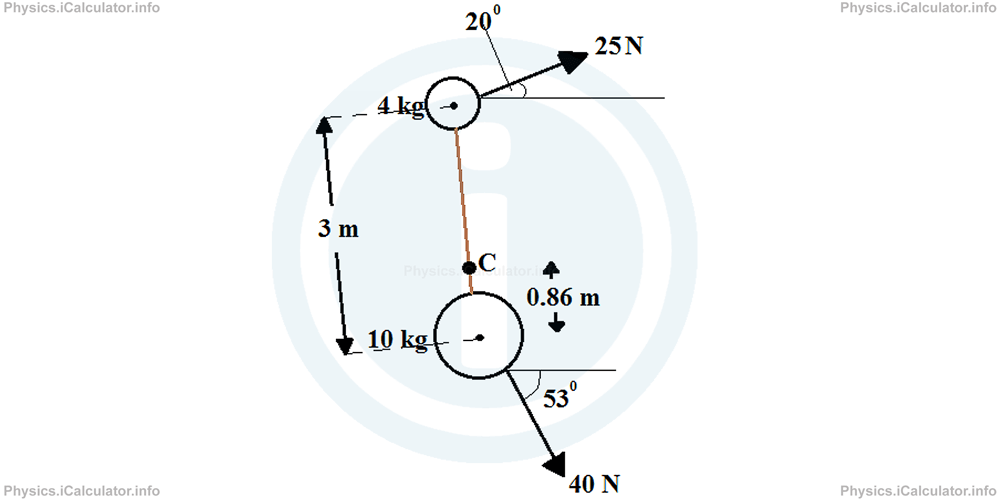
b. Now, let's calculate the resultant forces for each direction (now we take the horizontal direction as x and the vertical as y as usual). Also we take right as positive and left as negative for the x-direction and up as positive and down as negative for the y-direction as shown in the figure.
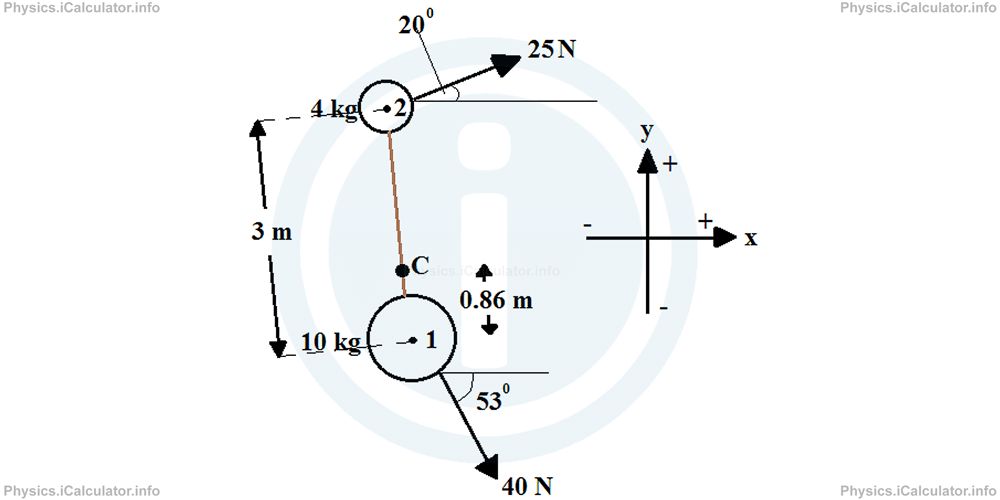
If we take the first angle as -530 and the second angle as 200, we have:
F1y = -|F1| × sin(-53)0 = 40 × (-0.80) = -32 N
F2x = |F2| × cos200 = 25 × 0.94 = 23.5 N
F2y = |F2| × sin200 = 25 × 0.34 = 8.5 N
(The minus sign mean that force is exerted in the negative direction)
Hence, we obtain for the resultant forces in each direction acting on the system
FRy = F1y + F2y = -32 N + 8.5 N = -23.5 N
Given that
= 10 kg + 4 kg
= 14 kg
We obtain for the corresponding accelerations of the system in each direction:
ay(sys) = FRy/msys = -23.5 N/14 kg = -1.68 m/s2
Therefore,
= √3.392 + (-1.68)2
= √11.49 + 2.82
= √14.31
= 3.78 m/s2
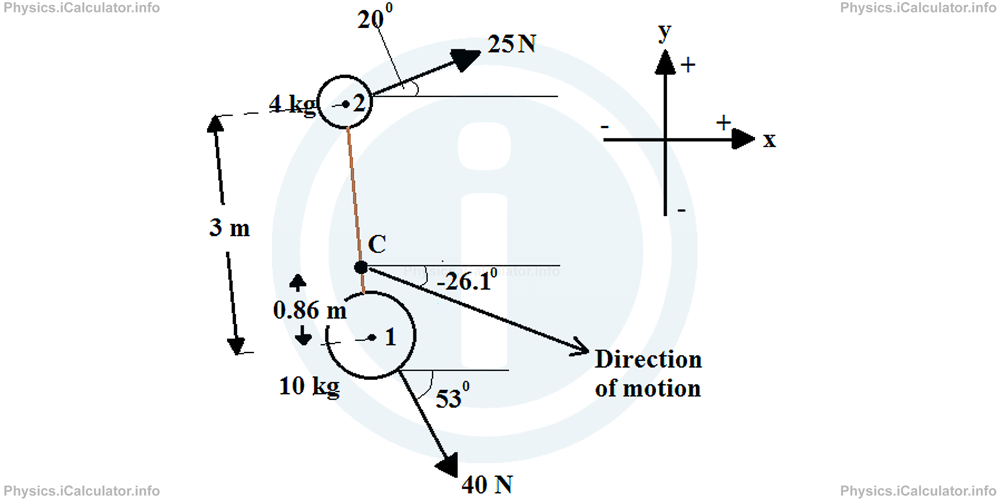
If we want to find the direction of motion, we consider again the centre of mass of the system. This is because the system's movement may be a combination of many basic motions such as linear, circular, vibrational, etc. Therefore, it would be quite impossible to study what happens with each individual particle of the system.
From Dynamics, we know that objects move in the direction of the resultant force acting on them. The same is true for systems of particles as well. Hence, we can find the direction of motion of the system's centre of mass by finding the direction of resultant force. For this goal, we must calculate the angle θ formed by the resultant force to the horizontal direction. We know that
The angle θ, which corresponds to this tangent value, is
= -26.10
= 3600 - 26.10
= 333.90
This means the acceleration (and the motion as well) is according the vector which is at 333.90 (or -26.10) to the horizontal direction as shown in the figure below.
You have reached the end of Physics lesson 6.3.1 Newton's Second Law for a System of Two Particles. There are 2 lessons in this physics tutorial covering Newton's Second Law for System of Particles, you can access all the lessons from this tutorial below.
More Newton's Second Law for System of Particles Lessons and Learning Resources
Whats next?
Enjoy the "Newton's Second Law for a System of Two Particles" physics lesson? People who liked the "Newton's Second Law for System of Particles lesson found the following resources useful:
- Two Particles Feedback. Helps other - Leave a rating for this two particles (see below)
- Centre of Mass and Linear Momentum Physics tutorial: Newton's Second Law for System of Particles. Read the Newton's Second Law for System of Particles physics tutorial and build your physics knowledge of Centre of Mass and Linear Momentum
- Centre of Mass and Linear Momentum Revision Notes: Newton's Second Law for System of Particles. Print the notes so you can revise the key points covered in the physics tutorial for Newton's Second Law for System of Particles
- Centre of Mass and Linear Momentum Practice Questions: Newton's Second Law for System of Particles. Test and improve your knowledge of Newton's Second Law for System of Particles with example questins and answers
- Check your calculations for Centre of Mass and Linear Momentum questions with our excellent Centre of Mass and Linear Momentum calculators which contain full equations and calculations clearly displayed line by line. See the Centre of Mass and Linear Momentum Calculators by iCalculator™ below.
- Continuing learning centre of mass and linear momentum - read our next physics tutorial: Moment of Force. Conditions of Equilibrium
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Newton's Second Law for System of Particles" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.