Physics Tutorial 9.4 - Gas Pressure

There are 6 lessons in this physics tutorial covering Gas Pressure. The tutorial starts with an introduction to Gas Pressure and is then followed with a list of the separate lessons, the tutorial is designed to be read in order but you can skip to a specific lesson or return to recover a specific physics lesson as required to build your physics knowledge of Gas Pressure. you can access all the lessons from this tutorial below.

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 2 Votes ]

In this Physics tutorial, you will learn:

The composition of atmosphere
What is air pressure?
How to measure air pressure?
What are the units used for measuring air pressure?
Why mercury is used as a capillary liquid in barometers?
How to measure a specific gas pressure?
How to calculate the total pressure in water?
How does the Atmospheric Pressure Vary with Altitude?

Introduction

Try this simple experiment at home, if you can.

Take a newspaper and unfold it.
Place the unfolded newspaper on a table as shown in the figure.
Put a plastic ruler above the table but under the newspaper. Leave half of the ruler uncovered and outside the table.
Kick or hit the uncovered part of the ruler upwards very quickly. What happens?

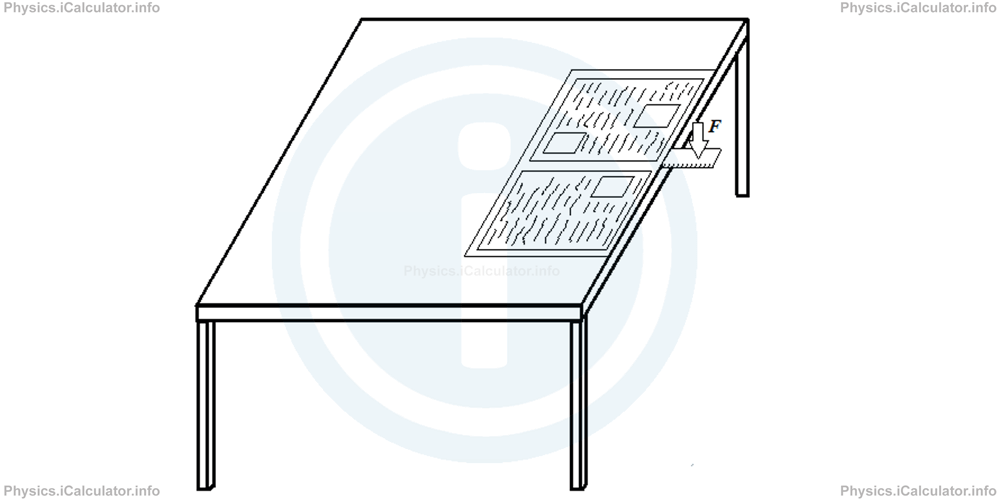
Physics Tutorials: This image provides visual information for the physics tutorial Gas Pressure

If you do the experiment according the instructions, i.e. if you kick the ruler very fast, it will break in two pieces. This is because air pressure above the newspaper prevents it to raise up immediately. As a result, the newspaper will block the part of the ruler under it. But if you kick the ruler slowly, you will give time to the air to enter under the newspaper and as a result, the air pressure is balanced in both sides of the newspaper. The ruler eventually will not break but it simply falls on the ground.

This experiment is an evidence of the air pressure strength, which people often underestimate. However, air pressure is an important part of our life. Therefore, in this tutorial we will discuss extensively about the pressure of air and other gases as well.

Please select a specific "Gas Pressure" lesson from the table below, review the video tutorial, print the revision notes or use the practice question to improve your knowledge of this physics topic.

Density and Pressure Learning Material
Tutorial ID	Physics Tutorial Title	Revision Notes	Revision Questions
9.4	Gas Pressure
Lesson ID	Physics Lesson Title	Lesson	Video Lesson
9.4.1	Air as a Mixture of Gases
9.4.2	Air (Atmospheric) Pressure
9.4.3	Why is Mercury Used as Capillary Liquid in Barometers?
9.4.4	Gas Pressure
9.4.5	Total Pressure in Water
9.4.6	How does the Atmospheric Pressure Vary with Altitude?

Whats next?

Enjoy the "Gas Pressure" physics tutorial? People who liked the "Gas Pressure" tutorial found the following resources useful:

Physics tutorial Feedback. Helps other - Leave a rating for this tutorial (see below)
Density and Pressure Revision Notes: Gas Pressure. Print the notes so you can revise the key points covered in the physics tutorial for Gas Pressure
Density and Pressure Practice Questions: Gas Pressure. Test and improve your knowledge of Gas Pressure with example questins and answers
Check your calculations for Density and Pressure questions with our excellent Density and Pressure calculators which contain full equations and calculations clearly displayed line by line. See the Density and Pressure Calculators by iCalculator™ below.
Continuing learning density and pressure - read our next physics tutorial: Buoyancy. Archimedes' Principle

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 2 Votes ]

Density and Pressure Calculators

The following Physics Calculators are provided in support of the Density and Pressure tutorials.

Physics Calculators

You may also find the following Physics calculators useful.

Menu

Physics Tutorial 9.4 - Gas Pressure

Introduction

Whats next?

Density and Pressure Calculators

Physics Calculators