Menu
Physics Lesson 14.7.4 - Energy Stored in a Charged Capacitor
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Energy Stored in a Charged Capacitor, this is the fourth lesson of our suite of physics lessons covering the topic of Capacitance and Capacitors, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Energy Stored in a Charged Capacitor
The source (here the battery) does some work to charge a capacitor from 0 to Q (i.e. increasing the charge of capacitor by ΔQ). As discussed in the previous tutorials of this section, the work W needed for such a process is
This process brings a uniform increase of the charge as shown in the graph below.
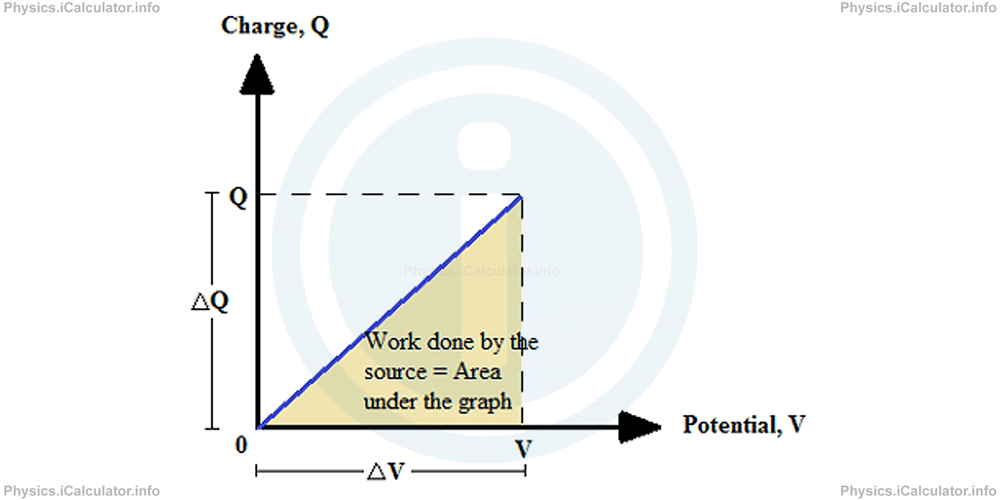
It is clear that the area under the graph represents the work done by the source to charge the capacitor. Since the figure under the graph is a right triangle, whose area is A = a × b / 2, we obtain for the work done by the source to charge the capacitor
where Q is the charge when the capacitor is fully charged.
As stated earlier in this chapter, the work done on a system contributes in the increase of its potential energy. This is also true in the specific case, i.e. the work done by the source to charge the capacitor from 0 to Q brings an increase in the potential energy of capacitor from 0 to PE. Therefore, we obtain for the electric potential energy stored in a charged capacitor:
We can transform the above equation into other forms using the capacitor formula C = Q /ΔV. Thus, we can write
= (C × ∆V) × ∆V/2
= C × ∆V2/2
and
= Q × Q/C/2
= Q2/2C
Obviously, all these formulae are equivalent as they are obtained through equivalent transformations.
Example 8
Two capacitors C1 = 60 nF and 30 nF are connected to the terminals of a 12 V battery as shown in the figure below.
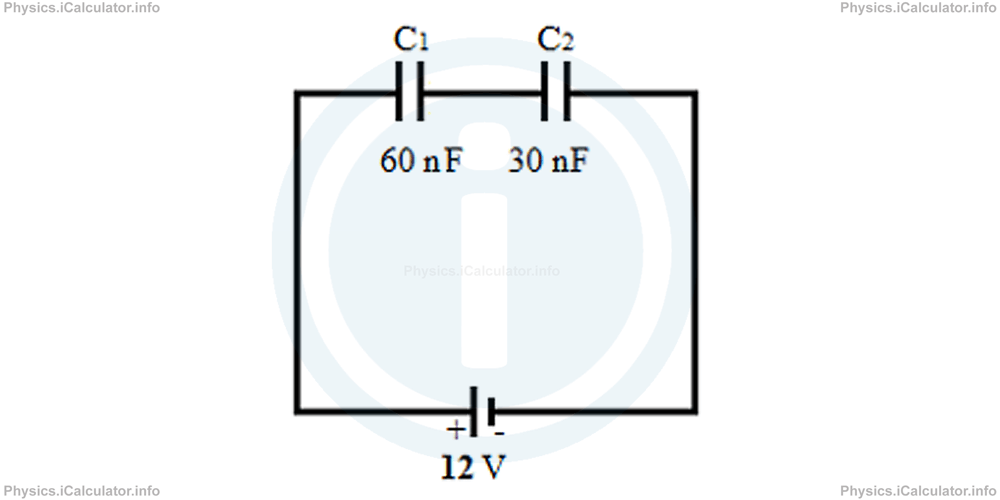
- What is the energy stored in the system?
- What is the energy stored in the capacitor C1?
- Stored Energy Feedback. Helps other - Leave a rating for this stored energy (see below)
- Electrostatics Physics tutorial: Capacitance and Capacitors. Read the Capacitance and Capacitors physics tutorial and build your physics knowledge of Electrostatics
- Electrostatics Revision Notes: Capacitance and Capacitors. Print the notes so you can revise the key points covered in the physics tutorial for Capacitance and Capacitors
- Electrostatics Practice Questions: Capacitance and Capacitors. Test and improve your knowledge of Capacitance and Capacitors with example questins and answers
- Check your calculations for Electrostatics questions with our excellent Electrostatics calculators which contain full equations and calculations clearly displayed line by line. See the Electrostatics Calculators by iCalculator™ below.
- Continuing learning electrostatics - read our next physics tutorial: Electric Charges. Conductors and Insulators
Solution 8
a) The total capacitance of this system of capacitors connected in series is
= 1/60 nF + 1/30 nF
= 1 + 2/60
= 3/60
Thus,
= 20 nF
Therefore, the energy stored in the system is
= 20 nF × (12 V)2/2
= 1440 nJ
= 1.44 μJ
= 1.44 × 10-6 J
b) The capacitor C1 carries the same charge as the entire system as it is connected in series with C2. But first, we must find this charge using the capacitor formula. We have
= Cs × ∆V
= 20 nF × 12 V
= 240 nC
= 2.4 × 10-7 C
Therefore, we obtain for the energy stored in the capacitor C1 (we have C1 = 60 nF = 6 × 10-8 F):
= (2.4 × 10-7 C)2/2 × 6 × 10-8 F
= 0.48 × 10-6 J
= 4.8 × 10-7 J
You have reached the end of Physics lesson 14.7.4 Energy Stored in a Charged Capacitor. There are 4 lessons in this physics tutorial covering Capacitance and Capacitors, you can access all the lessons from this tutorial below.
More Capacitance and Capacitors Lessons and Learning Resources
Whats next?
Enjoy the "Energy Stored in a Charged Capacitor" physics lesson? People who liked the "Capacitance and Capacitors lesson found the following resources useful:
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Capacitance and Capacitors" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.