Physics Lesson 3.7.4 - Average and Instantaneous Acceleration

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

Welcome to our Physics lesson on Average and Instantaneous Acceleration, this is the fourth lesson of our suite of physics lessons covering the topic of The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.

Average and Instantaneous Acceleration

As we have stated in the tutorial Speed and Velocity in One Direction, rarely occurs that an object keeps moving at the same velocity during the entire motion. The same thing can be said for the constant acceleration as well. It is quite impossible an object keeps accelerating at the same rate during its motion, as many other factors such as the resistive forces caused by the air etc., are not constant. We will see in the Physics tutorial Types of Forces II. Resistive Forces (Frictional Force. Drag). Terminal Velocity that air resistance increases when an object is moving faster than before. This brings a decrease in the acceleration until it becomes zero. As a result, the object successively will move at constant velocity.

Another similar example consists in a scenario in which a driver presses the brakes near the traffic lights and after a while (when the green light turns on), he presses the gas pedal. It is obvious this is an irregular motion although it may be rectilinear. This irregularity results in the impossibility to consider the motion as a whole. In this case, we can use one of the two following approaches:

1. Splitting the motion in small regular sections and finding the required quantities (here the acceleration) one by one before making any generalization, or
2. Considering the motion as a whole and calculating only the average values of the entire motion. In this tutorial, we are interested only in the average acceleration which is obtained by the following equation:

The second method is much shorter and easier because we need to know only three quantities: the two values of velocity (the initial and the final velocity) and the total time taken.

On the other hand, the instantaneous acceleration shows the acceleration at a given instant, similarly to the instantaneous velocity we discussed in the previous tutorials. Thus, if we are required to find the instantaneous acceleration in a certain instant t, we need to consider a very narrow time interval Δt around the given instant and calculating the respective velocities v⃗₁ and v⃗₂ for the two bordering points of the interval. Then, using the equation

we find the value of the instantaneous acceleration.

To help understand this point, a velocity vs time graph is shown below.

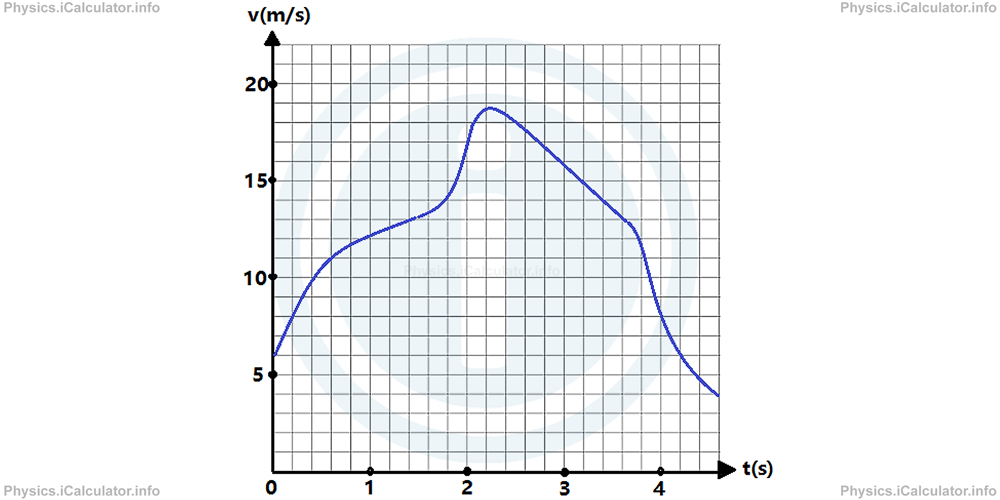
Let's suppose we are required to find the average acceleration t = 1.0 s. For this, we have to consider two surrounding points close to the given coordinate. For example, we can take t₁ = 0.6 s and t₂ = 1.4 s. Therefore, Δt = t₂ - ₁ = 1.4 s - 0.6 s = 0.8 s.

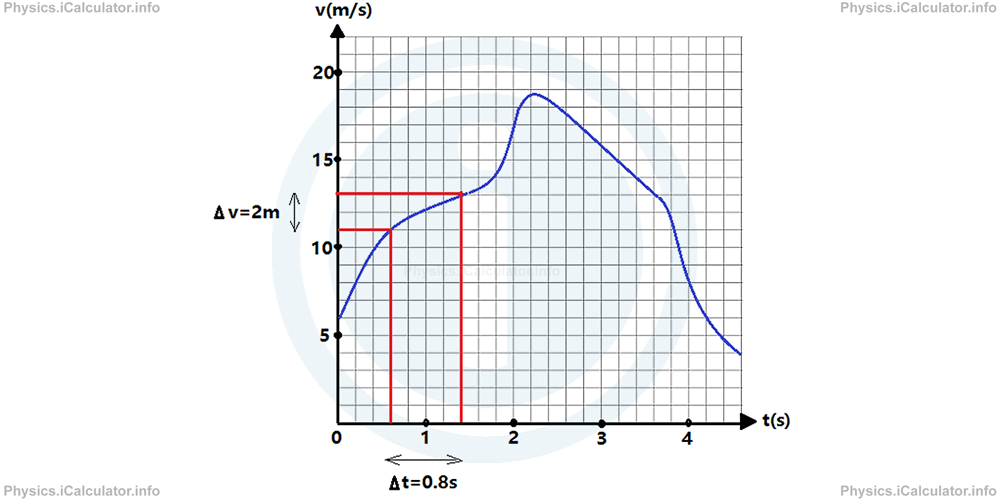
From the graph, it is easy to find that the respective values of velocity for these time values are v⃗₁ = 11 m/s and v⃗₂ = 13 m/s. Hence, we obtain for the instantaneous velocity in the given interval:

Example 1

An object starts moving from rest and it reaches a velocity of 16 m/s in 8 seconds. Then, it starts decelerating for the next 10 seconds until it comes to rest again.

Calculate:

1. The average acceleration during the first interval (during the first 8s)
2. The average acceleration during the second interval (during the next 10s)
3. The total average acceleration

Solution 1

The initial velocity is usually written in problems as u⃗ or v⃗₀; it is rarely written as v⃗₁ or v⃗_i. Also, the final velocity is often written as v⃗ instead of v⃗₂ or v⃗_f. Therefore, we can write the following values as clues:

We have to find < a⃗₁ >, < a⃗₂ > and < a⃗_tot > because we are not sure about how the object has moved; we only know the three values of velocity. No information regarding any possible motion with constant acceleration is provides. For this reason, we can only calculate the average values of acceleration, not the instantaneous acceleration in any section of motion.

The average acceleration during the first interval is:

The average acceleration during the second interval is:

Since the initial and final velocities are both zero, the total average acceleration is:

This is obvious because the positive acceleration in the first interval is cancelled out by the negative acceleration in the second interval.

Be careful to avoid taking the arithmetic mean of the two accelerations as in this case you get a wrong result. The only case in which it is allowed to calculate the average acceleration by finding the arithmetic mean is when the time intervals are equal.

You have reach the end of Physics lesson 3.7.4 Average and Instantaneous Acceleration. There are 5 lessons in this physics tutorial covering The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration, you can access all the lessons from this tutorial below.

More The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration Lessons and Learning Resources

Whats next?

Enjoy the "Average and Instantaneous Acceleration" physics lesson? People who liked the "The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration lesson found the following resources useful:

1. Average Feedback. Helps other - Leave a rating for this average (see below)
2. Kinematics Physics tutorial: The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration. Read the The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration physics tutorial and build your physics knowledge of Kinematics
3. Kinematics Revision Notes: The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration. Print the notes so you can revise the key points covered in the physics tutorial for The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration
4. Kinematics Practice Questions: The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration. Test and improve your knowledge of The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration with example questins and answers
5. Check your calculations for Kinematics questions with our excellent Kinematics calculators which contain full equations and calculations clearly displayed line by line. See the Kinematics Calculators by iCalculator™ below.
6. Continuing learning kinematics - read our next physics tutorial: Equations of Motion

Help others Learning Physics just like you

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

We hope you found this Physics lesson "The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.

Kinematics Calculators by iCalculator™

• Uniform Motion Calculator
• Uniformerly Accelerated Decelerated Motion Calculator
• Projectile Motion Calculator