Menu
Physics Lesson 3.7.3 - Constant and non-constant acceleration
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Constant and non-constant acceleration, this is the third lesson of our suite of physics lessons covering the topic of The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Constant and non-constant acceleration
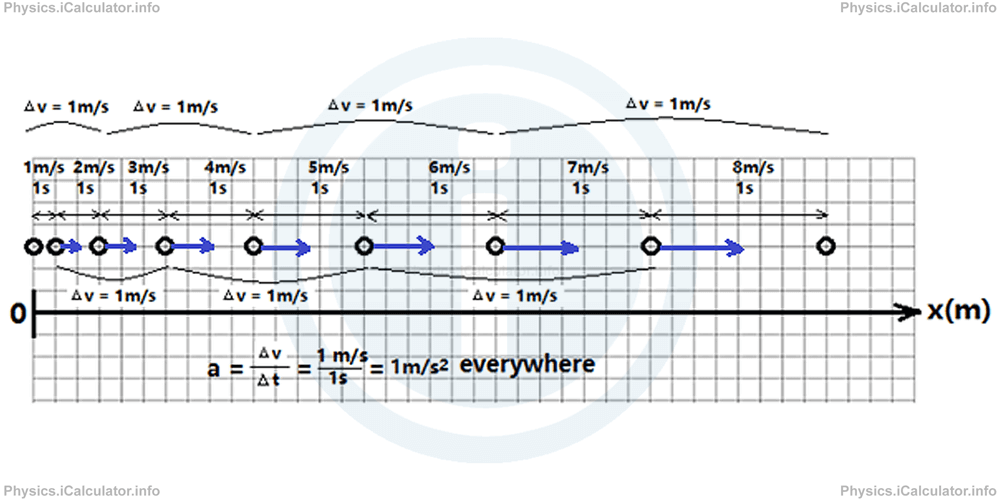
If we take the time intervals equal to 1s each in the motion map shown above, we can use numbers to understand better the meaning of acceleration. Thus, during the first second, the ball has moved due right by 1m, during the next seconds by 2m, during the third second by 3m and so on. This means the (average) velocity during the first second is 1m/1s = 1m/s, during the next second it is 2m/1s = 2m/s, during the third second it is 3m/1s = 3m/s and so on. Hence, it is obvious the velocity increases by 1m/s in every successive time interval (here 1s) compared to the previous one. Thus, the acceleration in our example is 1m/s2.
We have:
v⃗2 - v⃗1 = 2 m/s - 1 m/s = 1 m/s
v⃗3 - v⃗2 = 3 m/s - 2 m/s = 1 m/s
v⃗4 - v⃗3 = 4 m/s - 3 m/s = 1 m/s
and so on. Thus, since each time interval is ∆t=1s, we have for the acceleration in each interval:
a⃗2 = v⃗2 - v⃗1/∆t = 2 m/s - 1 m/s/1s= 1 m/s/1s= 1 m/s2
a⃗3 = v⃗3 - v⃗2/∆t = 3 m/s - 2 m/s/1s= 1 m/s/1s= 1 m/s2
a⃗4 = v⃗4 - v⃗3/∆t = 4 m/s - 3 m/s/1s= 1 m/s/1s= 1 m/s2
and so on. Therefore, it is obvious that in this example the increase in velocity occurred at the same rate. This means the acceleration - or as otherwise known, the rate of velocity change (here, the rate of velocity increase) - is constant (here, a = 1m/s2 in each interval). Hence, the situation described in the motion map discussed above, represents a "motion with constant acceleration."
Look at the motion map again. Now it includes the numerical values to make clearer the concept of acceleration and the reason why it is constant in the specific case.
On the other hand, if the object slows down, we say it is decelerating. Deceleration is the opposite of acceleration, i.e. it is a "negative acceleration." In such cases, the velocity decreases with time, i.e. the values of velocity in the successive intervals are smaller than those in the previous ones. This means the change in velocity is negative as in the expression ∆v⃗ = v⃗i + 1 - v⃗i (where i represents the number of the interval considered), the successive value of velocity (v⃗i + 1) is smaller than the previous one (v⃗i). Thus, when dividing a negative number (∆v⃗) by a positive one (Δt) the result is negative.
Let's take a look at another motion map to make this concept clear.
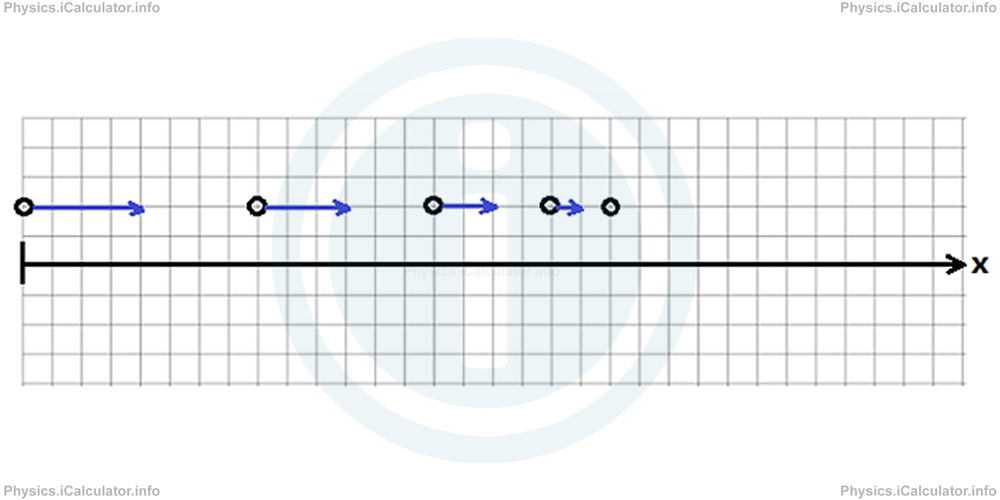
The arrow lengths become shorter and shorter until there is no arrow appearing in the figure. This means the ball stops at that position. If we appoint some values to the time intervals (for convenience, we can take them as Δt = 1s), and one unit in the graph is equal to 1m, we have for the average velocity during the first second:
In the next second, we have
In the third second, we have
In the fourth second, we have
and in the fifth (and the last) second, we have
Thus, the acceleration in each interval is
a⃗ = v⃗2-v⃗1/∆t = 4 m/s - 6 m/s/1s= -2 m/s/1s= -2 m/s2
a⃗ = v⃗2-v⃗1/∆t = 2 m/s - 4 m/s/1s= -2 m/s/1s= -2 m/s2
a⃗ = v⃗2-v⃗1/∆t = 0 m/s - 2 m/s/1s= -2 m/s/1s= -2 m/s2
From the results obtained, it is clear this is a uniformly decelerated motion as the acceleration is constant and negative.
You have reach the end of Physics lesson 3.7.3 Constant and non-constant acceleration. There are 5 lessons in this physics tutorial covering The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration, you can access all the lessons from this tutorial below.
More The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration Lessons and Learning Resources
Whats next?
Enjoy the "Constant and non-constant acceleration" physics lesson? People who liked the "The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration lesson found the following resources useful:
- Constant Feedback. Helps other - Leave a rating for this constant (see below)
- Kinematics Physics tutorial: The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration. Read the The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration physics tutorial and build your physics knowledge of Kinematics
- Kinematics Revision Notes: The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration. Print the notes so you can revise the key points covered in the physics tutorial for The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration
- Kinematics Practice Questions: The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration. Test and improve your knowledge of The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration with example questins and answers
- Check your calculations for Kinematics questions with our excellent Kinematics calculators which contain full equations and calculations clearly displayed line by line. See the Kinematics Calculators by iCalculator™ below.
- Continuing learning kinematics - read our next physics tutorial: Equations of Motion
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "The Meaning of Acceleration. Constant and Non-Constant Acceleration. Gravitational Acceleration" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.