Menu
Physics Lesson 3.5.2 - The meaning of Average and Instantaneous Speed
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on The meaning of Average and Instantaneous Speed, this is the second lesson of our suite of physics lessons covering the topic of Speed and Velocity in 1 Dimension, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
The meaning of Average and Instantaneous Speed
In the previous example, we found the speed of winner athlete was 5 m/s. It is obvious this represents an average value, as it is impossible for the athlete to keep moving at this speed during the entire race. Normally an athlete runs faster at the beginning of a race and then he slows down, as he gets tired. Therefore, we use the concept of "average speed" to represent a motion, which is presumably irregular.
By definition, "The average speed < v > of an object refers to the total distance it travels divided by the time elapsed."
Mathematically, we write
The utility of the average speed use is better observed in the following example.
Example 1
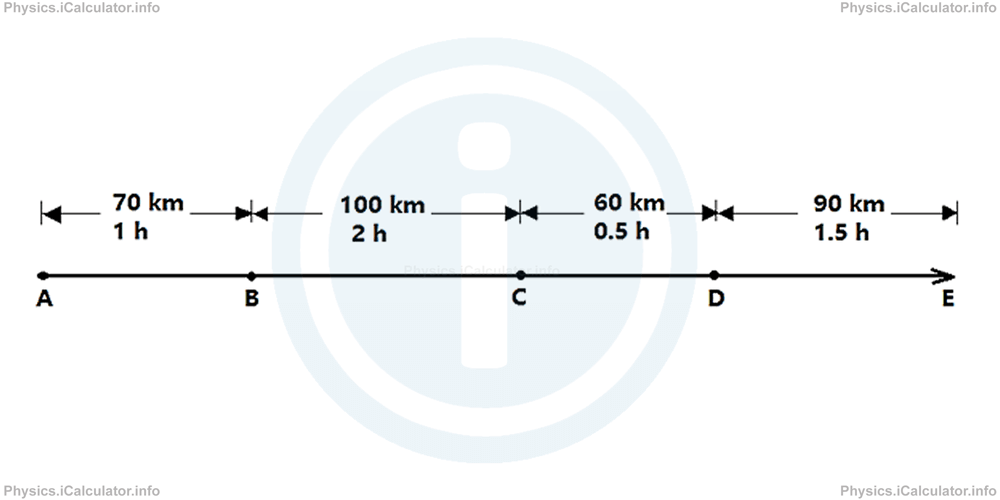
What is the average speed of the car (in km/h) during the entire trip?
Solution 1
It is obvious the motion has not been uniform during the trip. Therefore, we must use the concept of average speed to understand whether the car has moved fast or slowly during the process.
From the equation of the average speed
and relying on the data shown in the figure, we see that
Substituting the values, we obtain for the average speed of the car
= 320km/5h
= 64 km/h
On the other hand, Instantaneous Speed (v) is another important concept used in Kinematics. It shows the actual speed at which an object is moving. An example of application in daily life of the instantaneous speed concept is the car's speedometer. It shows the instantaneous speed of the car as it takes "live" measurements of the car's moving speed.
But how can we measure the instantaneous speed when an object is not doing a uniform motion and furthermore when its motion is quite irregular?
The procedure is not very simple. However, with the help of digital electronics this is a solved issue already. Basically, a very sensitive timer is used to partialize the motion in small intervals and for each interval the distance is calculated through a distance sensor. The speed cannot change drastically due to the object's "inertia" (look at the tutorial Newton's First Law of Motion. The Meaning of Inertia). Therefore, the average speed measured for each of the abovementioned small intervals of time represents the instantaneous speed of the object in that specific instant. The result obtained is accurate enough as any change in values is smooth considering the shortness of time intervals.
To calculate instantaneous speed, we need to divide the distance by time. However, we don't want to use the distance of the entire trip, because that will give us average speed. We take a small portion of distance and divide it by the corresponding (small) time interval. The smaller the distance (and the time interval) used, the more accurately we can measure the speed for that specific time.
The equation of instantaneous speed v is:
where Δs represents the small distance considered and Δt the time interval during which the event occurs.
If it is possible to represent the motion in a graph this would be a huge advantage as the value of the instantaneous speed is calculated directly from the data shown in the graph. Look at the example below.
Example 2
The following graph shows the dependence of the Distance travelled by an object from the Time elapsed. Find the speed of the object at t = 4.4 s.
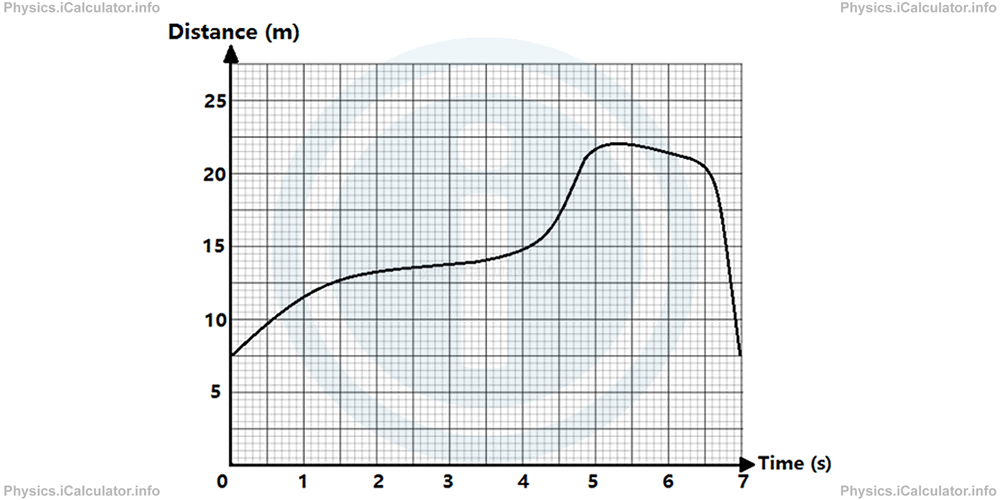
Solution 2
As explained before, we must take two neighbouring values for the distance (s1 and s2) and the time (t1 and t2), which must be as close as possible and then using the equation
to calculate the instantaneous speed at the required instant.
Let's take for example t1 = 4.1 s and t2 = 4.6 s. The corresponding distances for these two time values are s1 = 15.0 m and s2 = 18.0 m respectively. Look at the figure:
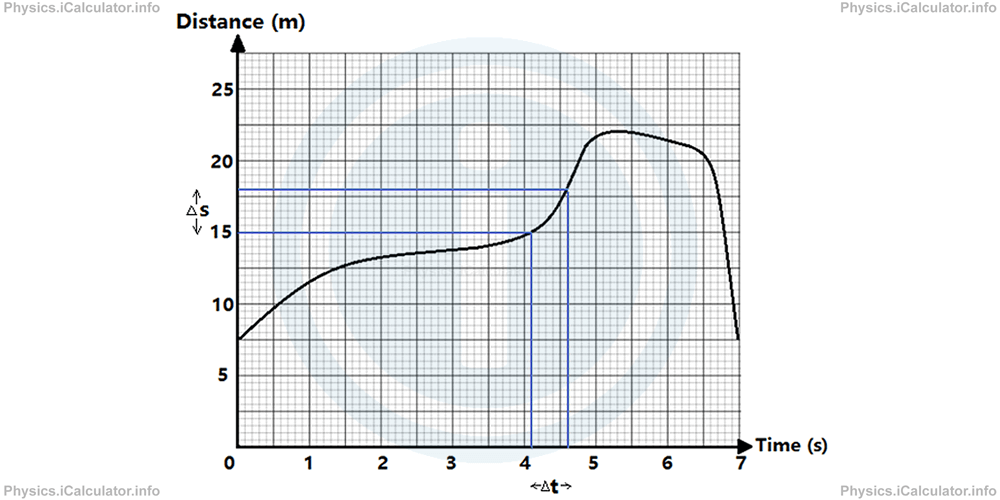
Therefore, we obtain for the instantaneous speed at t = 4.4 s or as it is otherwise written, v (4.4):
= s2-s1/t2-t1
= 18.0m - 15.0m/4.6s - 4.1s
= 3.0m/0.5s
=6 m/s
This is an approximate value, which becomes closer to the true value when the intervals become finer. However, it gives us a good idea on how the object is moving.
You have reach the end of Physics lesson 3.5.2 The meaning of Average and Instantaneous Speed. There are 4 lessons in this physics tutorial covering Speed and Velocity in 1 Dimension, you can access all the lessons from this tutorial below.
More Speed and Velocity in 1 Dimension Lessons and Learning Resources
Whats next?
Enjoy the "The meaning of Average and Instantaneous Speed" physics lesson? People who liked the "Speed and Velocity in 1 Dimension lesson found the following resources useful:
- Average Instantaneous Speed Feedback. Helps other - Leave a rating for this average instantaneous speed (see below)
- Kinematics Physics tutorial: Speed and Velocity in 1 Dimension. Read the Speed and Velocity in 1 Dimension physics tutorial and build your physics knowledge of Kinematics
- Kinematics Revision Notes: Speed and Velocity in 1 Dimension. Print the notes so you can revise the key points covered in the physics tutorial for Speed and Velocity in 1 Dimension
- Kinematics Practice Questions: Speed and Velocity in 1 Dimension. Test and improve your knowledge of Speed and Velocity in 1 Dimension with example questins and answers
- Check your calculations for Kinematics questions with our excellent Kinematics calculators which contain full equations and calculations clearly displayed line by line. See the Kinematics Calculators by iCalculator™ below.
- Continuing learning kinematics - read our next physics tutorial: Speed and Velocity in 2 and 3 Dimensions
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Speed and Velocity in 1 Dimension" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.