Physics Lesson 16.18.2 - Induced Magnetic Fields

Please provide a rating, it takes seconds and helps us to keep this resource free for all to use

★★★★★ [ 1 Votes ]

Welcome to our Physics lesson on Induced Magnetic Fields, this is the second lesson of our suite of physics lessons covering the topic of Maxwell Equations, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.

Induced Magnetic Fields

In the tutorial 16.7, we explained that a changing magnetic flux induces an electric field in a loop, which on the other hand generates an emf (and current) in the loop.

This represents the Faraday's Law and its integral form is

∮E⃗ dL⃗ = -dΦ_b/dt

The reverse is also true. A changing electric flux can induced a magnetic field. The equation representing this property is known as Maxwell Law of Induction and the corresponding equation is

∮B⃗ dL⃗ = μ₀ ∙ ε₀ ∙ dΦ_e/dt

Here B⃗ represents the magnetic field induced along a closed loop by means of the changing electric flux ΦE in the region enclosed by the loop.

For example, let's consider a parallel-plate capacitor with circular plates, the lateral and front view of which, are shown below.

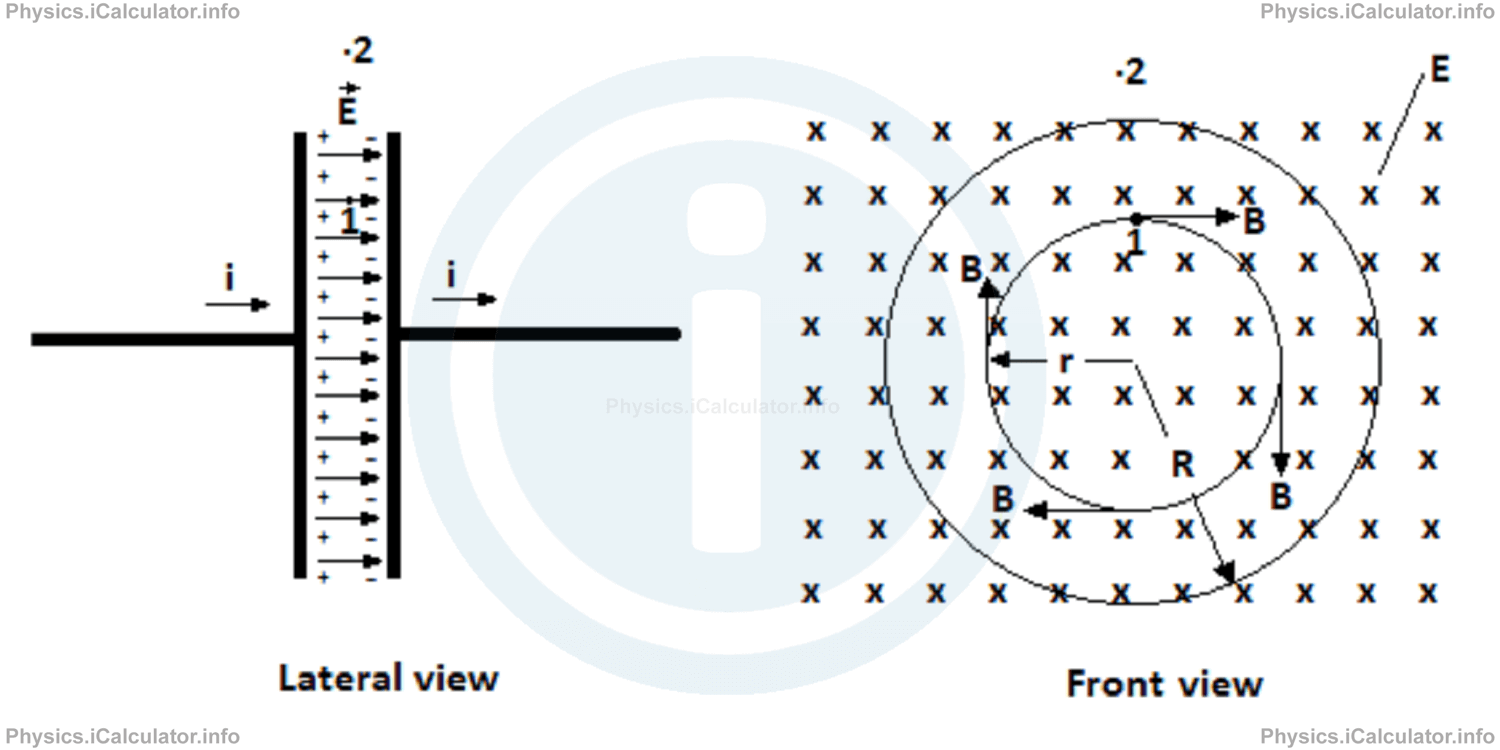
Physics Tutorials: This image provides visual information for the physics tutorial Maxwell Equations

The front view shows the right plate of the capacitor viewed from inside the plates.

If we assume the charge in the capacitor places increases at a steady rate through a constant current I in the conducting wire, a changing electric flux will occur in the plates - a process that will induce a magnetic field on the capacitor plates because the electric field between the plates changes at a steady rate as well. This induced magnetic field is circular because we may assume any Amperian loop as the border of a current-carrying wire and when using the right hand-rule, we obtain a circular magnetic field if the current carrying wire is straight.

In other words, if the circles having the radii r and R are through as radii of two current-carrying wires of different thickness, the corresponding magnetic fields will be circular, and their directions are found using the right-hand rule. In the specific case, since the current is inwards, the direction of thumb will be onto the page, while the other curled fingers will be oriented clockwise, as shown in front view of the above figure.

The same thing can be said when a circular (Amperian) current-carrying loop is taken inside a uniform magnetic field B. In this case, we obtain the following figure:

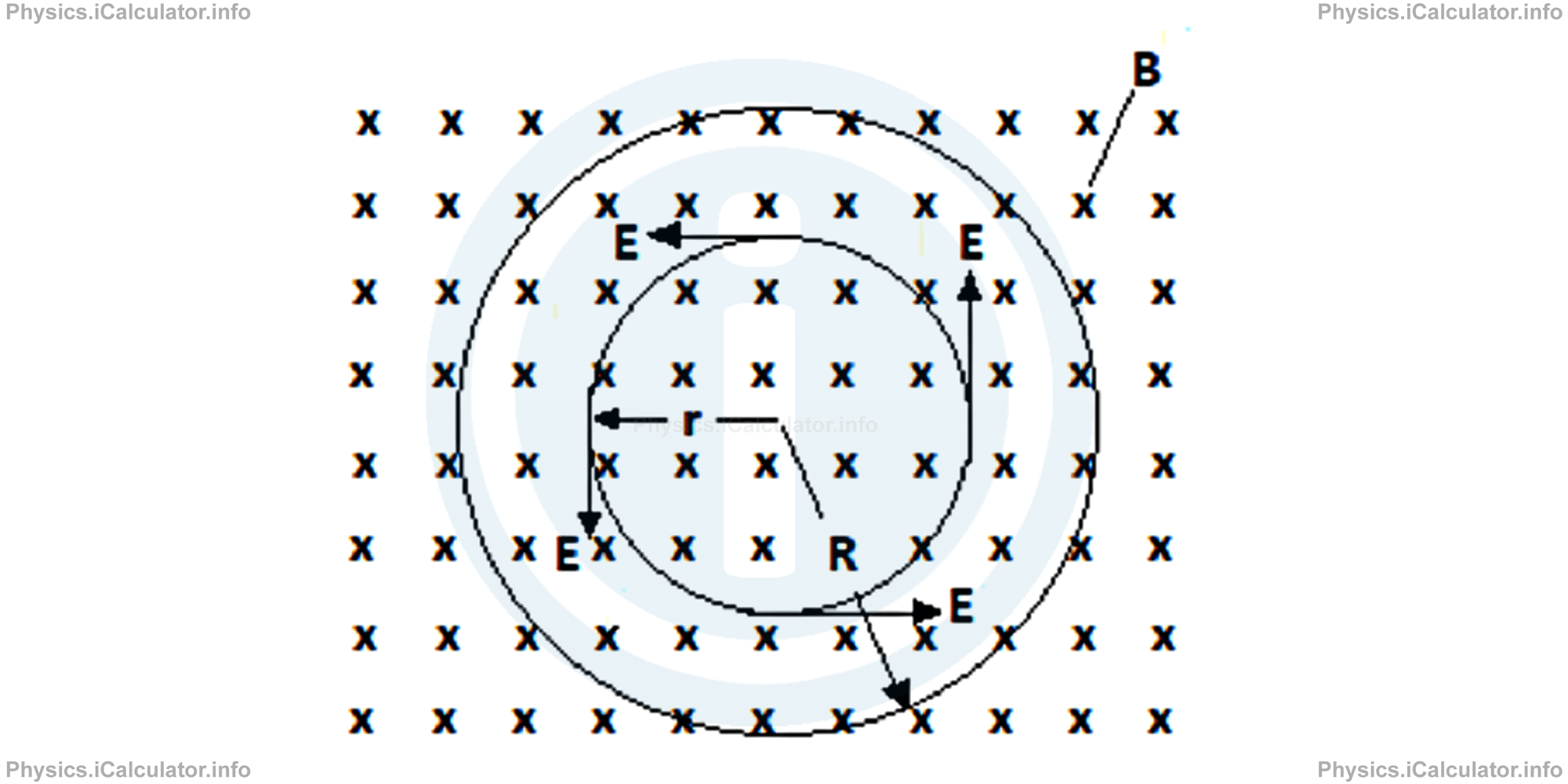
The only difference to the previous figure is that the direction of electric field here is anticlockwise.

The last two equations shown earlier are similar, as they both involve a closed integral (the integral taken along a closed loop), the result of which, involves the change of the other flux in the unit of time (B → dΦE and E → dΦB).

In other words, an increasing electric field E directed onto the page, induces a counter-clockwise magnetic field B in the loop, while an increasing magnetic field B directed onto the page, induces a counter-clockwise electric field E in the loop.

Combining the last two equations, we obtain the Ampere-Maxwell Law

∮B⃗ dL⃗ = μ₀ ∙ ε₀ ∙ dΦ_e/dt + μ₀ ∙ i_encl

As special cases, we can consider the two following scenarios:

When there is a current but no change in electric flux (such as a wire carrying a constant current), the first term on the right side of the Ampere-Maxwell Law is zero. As a result, the Ampere's Maxwell Law reduces to Ampere's law of Induction we have seen in tutorial 16.6.

∮B⃗ dL⃗ = μ₀ ∙ i_encl

When there is a change in electric flux but no current (such as inside or outside the gap of a charging capacitor), the second term on the right side of the Ampere-Maxwell Law becomes zero, and so the Ampere's Maxwell Law reduces to the Maxwell's Law of induction

∮B⃗ dL⃗ = μ₀ ∙ ε₀ ∙ dΦ_e/dt

Example 2

A circular-plate capacitor of plate radius R is being charged as shown in the figure below.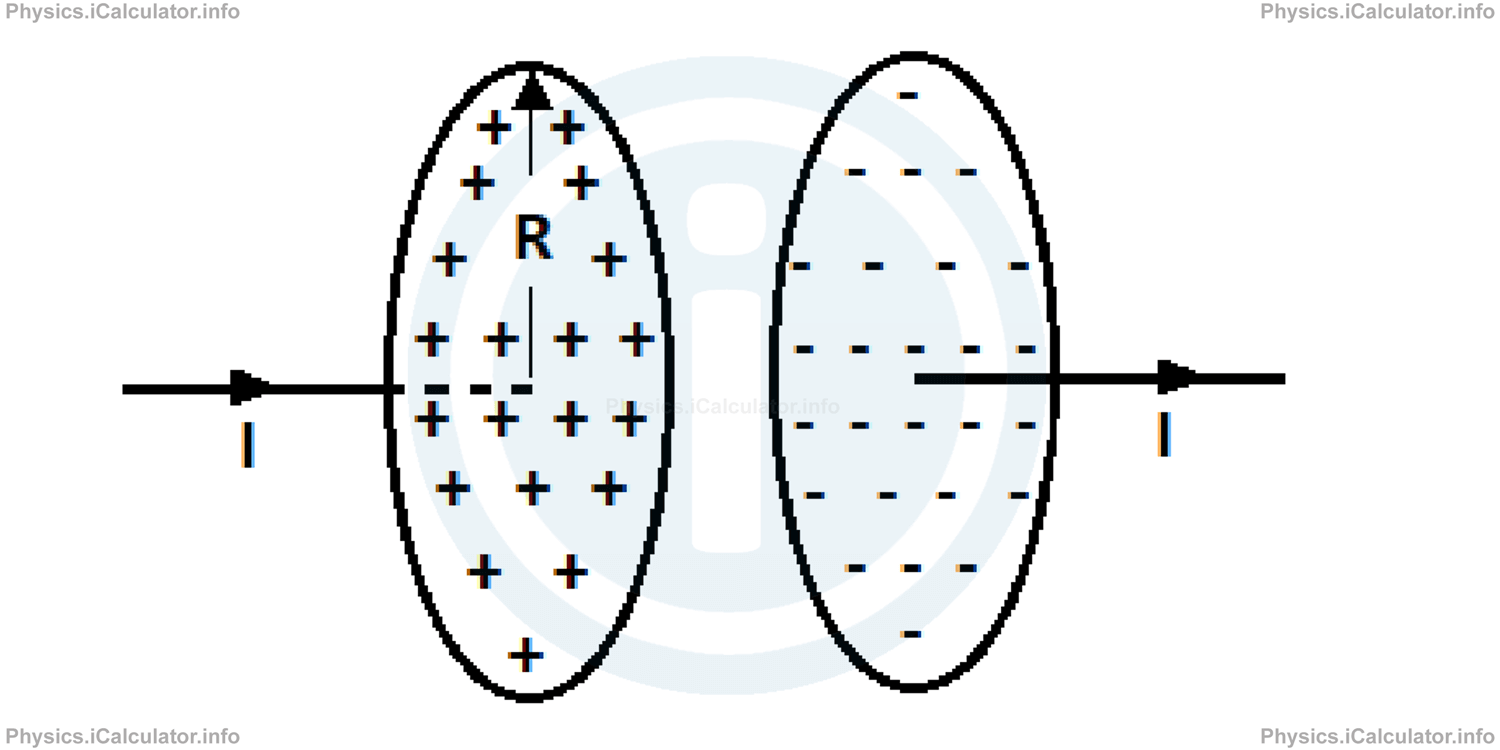

What is the magnetic field in terms of electric field for any r < R?
Calculate the magnetic field magnitude for r = 1/3 R = 6 cm and dE/dt = 4 × 1012 V/(m·s)
Calculate the maximum magnitude of magnetic field inside the plates of capacitor
Derive an expression for the magnetic field outside the capacitor (r > R) and calculate the magnitude of magnetic field at r = 25 cm from the centre of plates

Solution 2

From the equation representing the Ampere-Maxwell Law, we see that a magnetic field can be set up either by a current or by induction due to a changing electric flux (or from both factors combined together). In the specific case, we don't have any current flowing between the capacitor plates but anyway, the electric flux is changing due to the increase of opposite charges in both plates. Hence, the Ampere-Maxwell Law equation
∮B⃗ dL⃗ = μ₀ ∙ ε₀ ∙ dΦ_e/dt + μ₀ ∙ i_encl
reduces to the Maxwell's Law of induction
∮B⃗ dL⃗ = μ₀ ∙ ε₀ ∙ dΦ_e/dt
where B is the magnetic field, L is the length (perimeter) of the Amperian loop, ε0 and μ₀ are the electric and magnetic field constants respectively, and dΦE/dt is the change in the electric flux in the unit of time.
To derive an expression for the magnetic field in terms of electric field, we must consider separately the left and the right part of Maxwell's Law of induction.
For the left side, we consider an Amperian loop of radius r < R as shown in the figure, as we want to calculate the magnetic field inside the capacitor, i.e. for r ≤ R. As seen in theory, the magnetic field along the loop is tangent to it, in the same direction to the path element dL. They can either be parallel antiparallel but for simplicity we will assume them as parallel (cos θ = 0°), because this does not affect the result.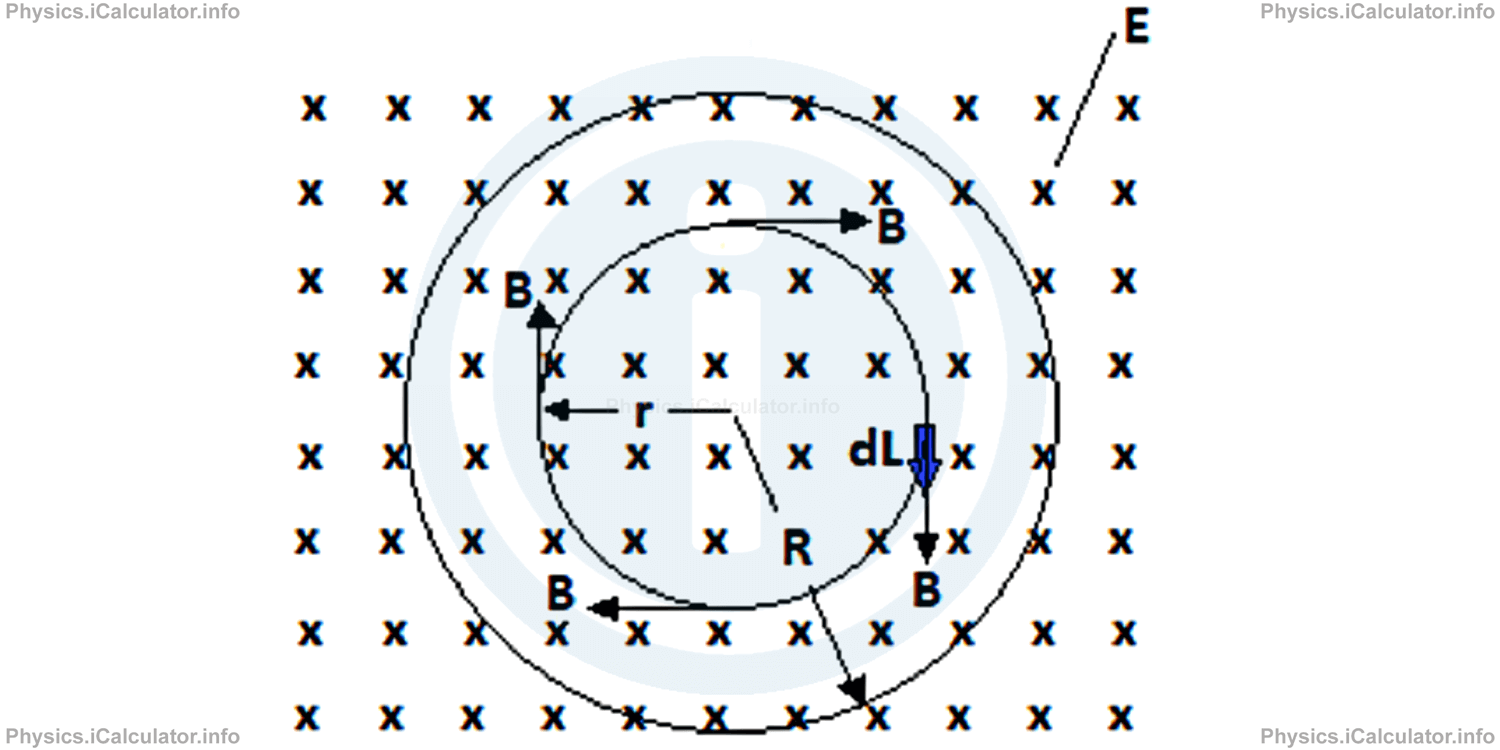 Thus, we can write:
∮B⃗ dL⃗ = ∮B dL ∙ cos⁡0⁰ = ∮B dL
Since the magnetic field is constant (the loop is symmetric), we obtain
∮B dL = B ∙ ∮dL
The expression inside the integral is simply the circumference of the circle formed by the Amperian loop considered. Thus, we have for the left side of the Maxwell Law of Induction applied in the specific case:
B ∙ ∮dL = B ∙ (2π ∙ r)
As for the right side of the equation representing the Maxwell law of induction, we assume the electric field E is uniform between the capacitor plates and perpendicular to them. This means the electric flux is the product of two constants: E and A where A is the area of the Amperian loop considered above. Thus, we can write:
Φ_e = E ∙ A
and the right side of the Maxwell Law of Induction becomes
μ₀ ∙ ε₀ ∙ dΦ_e/dt = μ₀ ∙ ε₀ ∙ d(E·A)/dt
Substituting the expressions obtained for each side of the Maxwell Law of Induction, we obtain
B ∙ (2π ∙ r) = μ₀ ∙ ε₀ ∙ d(E·A)/dt
Since the area of the Amperian loop considered here is constant and it is calculated by
A = π ∙ r²
we can write
B ∙ (2π ∙ r) = μ₀ ∙ ε₀ ∙ (π ∙ r² ) ∙ dE/dt
In this way, we can now derive an expression for magnetic field in terms of electric field (more precisely, in terms of the rate of change of the electric field):
B = μ₀ ∙ ε₀ ∙ r/2 ∙ dE/dt
The above expression indicates that the magnetic field inside the capacitor increases linearly with the change in distance from the centre of the plate (where the magnetic field is zero because r = 0) to the maximum value obtained at the outer frame of the plates (where r = R).
In this part of exercise we have the following clues:
r = 6 cm = 6 × 10^-2 m
R = 3r = 18 × 10^-2 m = 1.8 × 10^-1 m
dE/dt = 4 × 1012 V/(m·s)
Also, we know that
ε0 = 8.85 × 10^-12 C²/(N·m²)
μ₀ = 4π × 10^-7 N/A²
Thus, from the expression derived in (a), we obtain for the magnetic field B at the given distance r from the centre of capacitor plates:
B = μ₀ ∙ ε₀ ∙ r/2 ∙ dE/dt
= (4 ∙ 3.14 × 10^-7 N/A² ) ∙ (8.85 × 10^-12 C²/(N·m²)) ∙ (6 × 10^-2 m)/2 ∙ 4 × 10¹² V/m ∙ s
= 1.334 × 10^-6 T
The maximum magnetic field inside the plates is obtained for r = R. Thus, substituting the values in the equation used in (b), we obtain
B = μ₀ ∙ ε₀ ∙ r/2 ∙ dE/dt
It is not necessary to do again the operations as it is obvious that since the radius increases by a factor of 3, the magnetic field increases by the same factor as well. Thus, we obtain for the maximum magnetic field between the capacitor plates is
B_max = 3 ∙ B
= 3 ∙ 1.334 × 10^-6 T
= 4.0 × 10^-6 T
From previous tutorials, we known that electric field exists only between the plates of capacitor. This means that despite having a distance r > R from the centre of plates, the area to consider in the Maxwell equation is only A = π · r₂. Thus, since the left part of the equation
B ∙ (2π ∙ r) = μ₀ ∙ ε₀ ∙ (π ∙ r² ) ∙ dE/dt
does not change, we obtain after substituting r = R in the right side:
B ∙ (2π ∙ r) = μ₀ ∙ ε₀ ∙ (π ∙ R² ) ∙ dE/dt
B = μ₀ ∙ ε₀ ∙ (π ∙ R² ) ∙ dE/dt/(2π ∙ r)
= μ₀ ∙ ε₀ ∙ R² ∙ dE/dt/2r
Substituting the known values (here, r = 25 cm = 2.5 × 10^-1 m), we obtain for the magnetic field B:
B = (4 ∙ 3.14 × 10^-7 N/A² ) ∙ (8.85 × 10^-12 C²/(N·m²)) ∙ (1.8 × 10^-1m)² ∙ (4 × 10¹² V/m ∙ s)/(2 ∙ 2.5 × 10^-1m)
= 2.88 × 10^-6 T
As you see from the results, the magnetic field outside the capacitor decreases when the distance from the centre of plates increases. However, even between the plates the magnetic field is very small when compared to the magnitude of electric field. This is the reason why capacitors are considered as electric devices and not as magnetic ones.

You have reached the end of Physics lesson 16.18.2 Induced Magnetic Fields. There are 5 lessons in this physics tutorial covering Maxwell Equations, you can access all the lessons from this tutorial below.

More Maxwell Equations Lessons and Learning Resources

Magnetism Learning Material
Tutorial ID	Physics Tutorial Title	Revision Notes	Revision Questions
16.18	Maxwell Equations
Lesson ID	Physics Lesson Title	Lesson	Video Lesson
16.18.1	Gauss Law for Magnetic Field
16.18.2	Induced Magnetic Fields
16.18.3	Displacement Current
16.18.4	How to Find the Induced Magnetic Field?
16.18.5	Maxwell Equations Explained

Whats next?

Enjoy the "Induced Magnetic Fields" physics lesson? People who liked the "Maxwell Equations lesson found the following resources useful:

Induced Magnetic Fields Feedback. Helps other - Leave a rating for this induced magnetic fields (see below)
Magnetism Physics tutorial: Maxwell Equations. Read the Maxwell Equations physics tutorial and build your physics knowledge of Magnetism
Magnetism Revision Notes: Maxwell Equations. Print the notes so you can revise the key points covered in the physics tutorial for Maxwell Equations
Magnetism Practice Questions: Maxwell Equations. Test and improve your knowledge of Maxwell Equations with example questins and answers
Check your calculations for Magnetism questions with our excellent Magnetism calculators which contain full equations and calculations clearly displayed line by line. See the Magnetism Calculators by iCalculator™ below.
Continuing learning magnetism - read our next physics tutorial: Introduction to Magnetism

Help others Learning Physics just like you