Menu
Physics Lesson 7.2.3 - Moment of Inertia in Different Systems of Rotational Motion
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Moment of Inertia in Different Systems of Rotational Motion, this is the third lesson of our suite of physics lessons covering the topic of Dynamics of Rotational Motion, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Moment of Inertia in Different Systems of Rotational Motion
The main equation of moment of inertia I = m × r2 can take other forms based on the structure and shape of the rotating object involved. The formulae for all cases involved are found by integration. However, here it is not the case to deal so much with the method how these equations are obtained. We will simply provide the formulae for some common situations without losing time with the procedure.
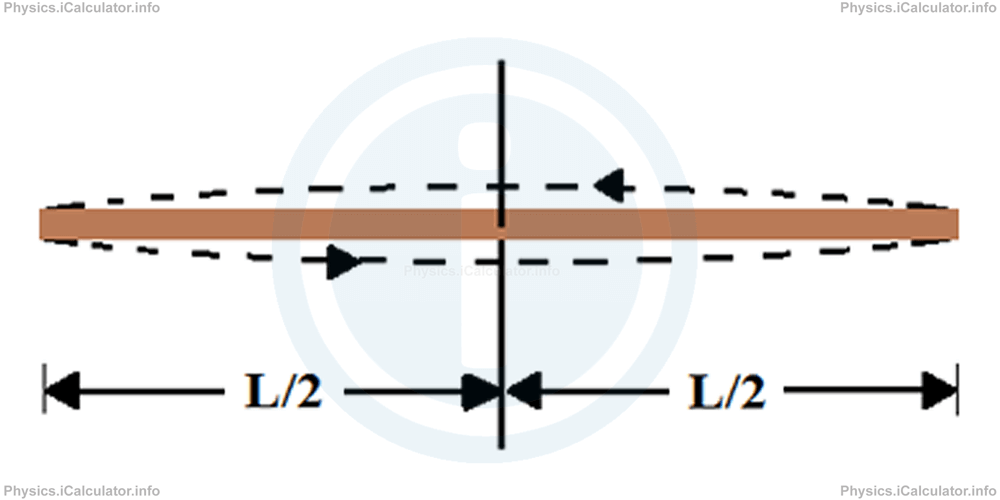
a. A long bar of length L rotating around its centre
Moment of inertia of a bar of mass m and length L when rotating around its centre as shown in the figure, is:
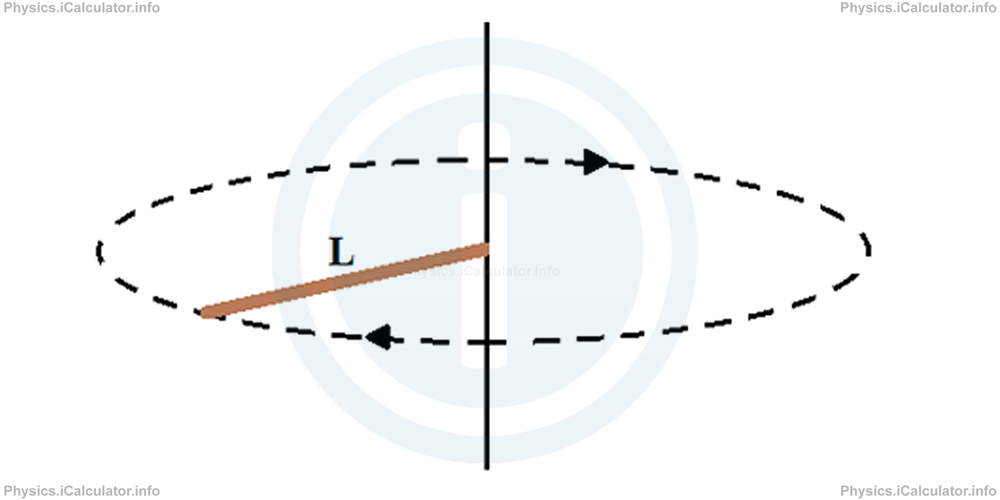
b. A long bar of length L rotating around its end
Moment of inertia of a bar of mass m and length L when rotating around its end as shown in the figure, is:
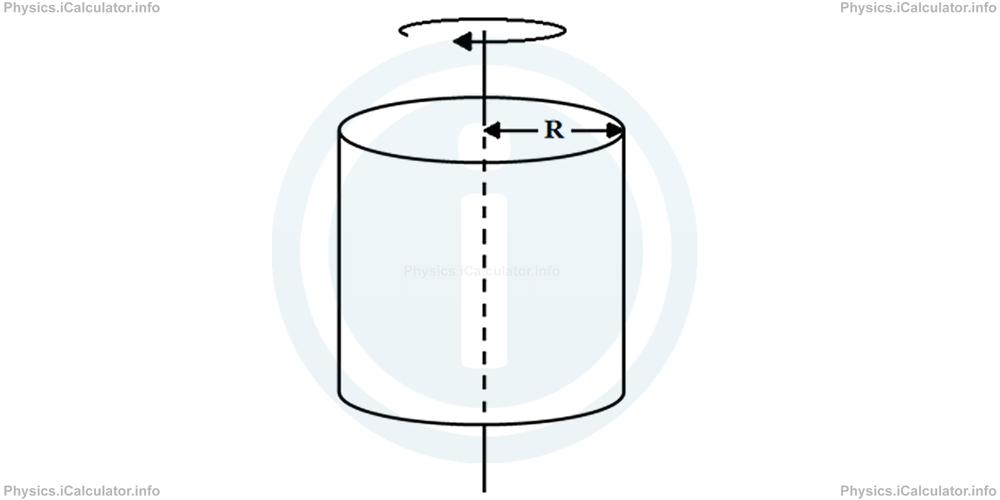
c. A solid cylinder or disc rotating around its symmetry axis
Moment of inertia of a cylinder or disc (a disc is a cylinder with a very short height compared to its base radius) of mass m and base radius R when rotating around its axis of symmetry, which passes along the height as shown in the figure, is:
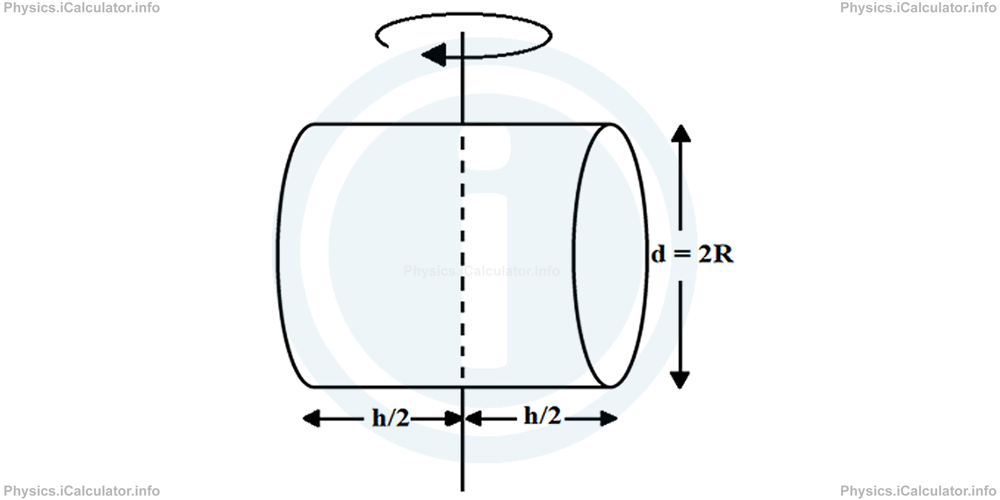
d. A solid cylinder or disc rotating around its central diameter
Moment of inertia of a cylinder or disc of mass m, height h and base radius R when rotating around its central diameter as shown in the figure, is:
e. A ring of radius R rotating around its symmetry axis
Moment of inertia of a ring of mass m and radius R when rotating around its axis of symmetry, which passes along the centre as shown in the figure, is:
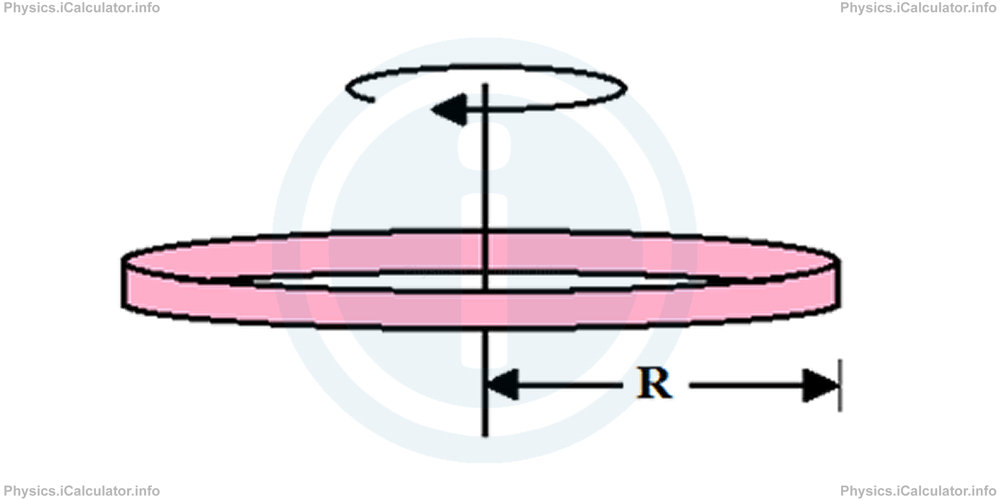
f. A ring of radius R rotating around its diameter
Moment of inertia of a ring of mass m and radius R when rotating around its diameter as shown in the figure, is:
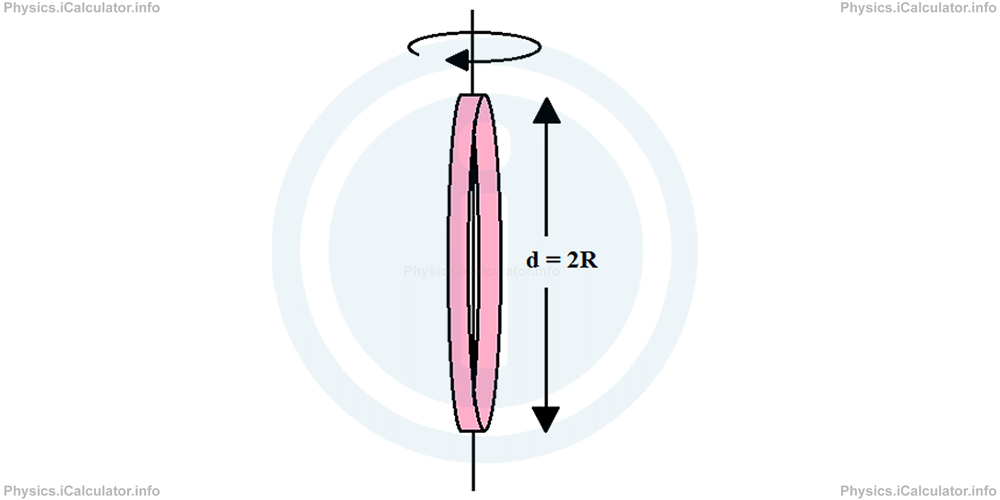
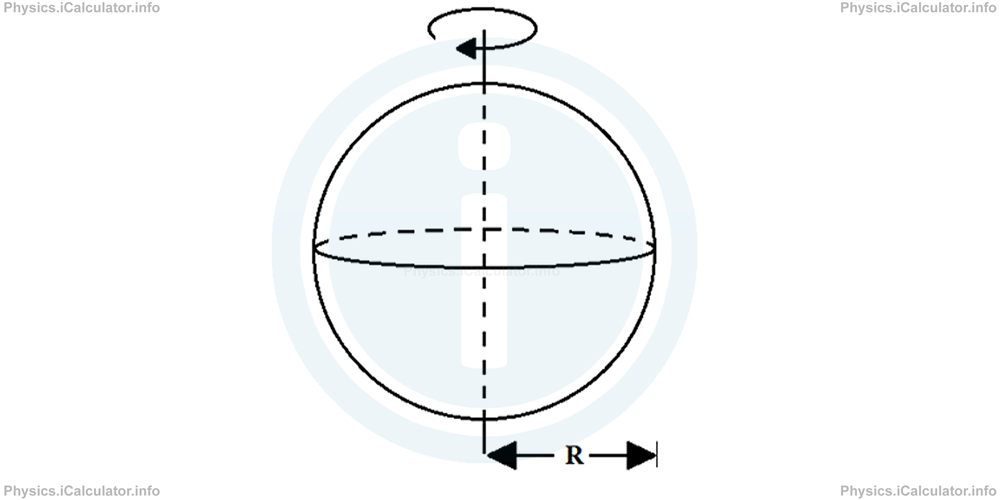
g. A solid sphere of radius R rotating around its central diameter
Moment of inertia of a sphere of mass m and radius R when rotating around its central diameter as shown in the figure, is:
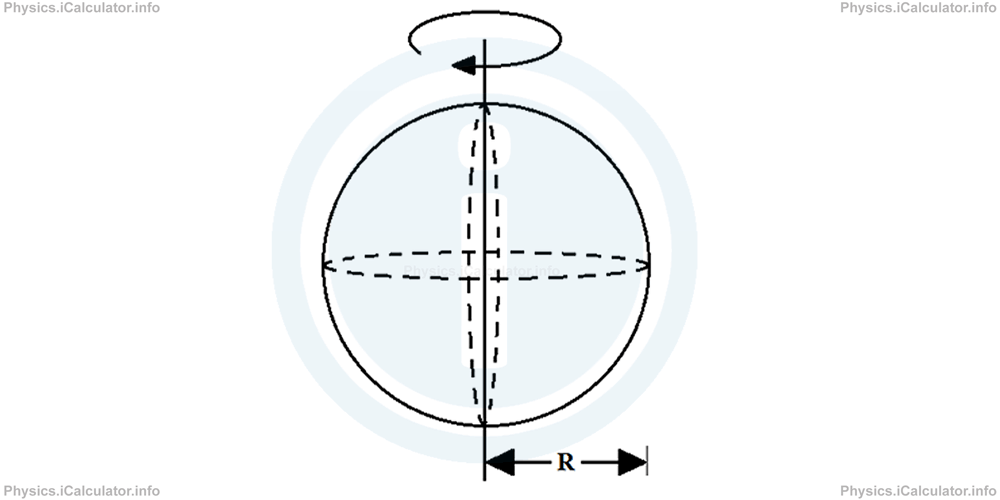
h. A thin spherical shell of radius R rotating around its central diameter
Moment of inertia of a spherical shell of mass m and radius R when rotating around its central diameter as shown in the figure, is:
Example 2
Calculate the moment of inertia for the following objects:
- A 12 m long metal wire of cross section diameter equal to 1 mm rotating around its centre. The mass of metal wire is 2 kg. Take the metal bar as not bendable.
- A 80 cm long wooden rod of diameter equal to 12 cm and mass equal to 400 g rotating around its central diameter.
- A 600 g hollow sphere of radius equal to 20 cm rotating around its central diameter.
Solution 2
a. Since the diameter of cross-sectional area is much smaller than the length of wire, we consider it as a long bar instead of a cylinder. Therefore, we neglect the wire's thickness and focus only on its length, i.e. we have L = 12 m and m = 2 kg. Therefore, applying the formula of moment of inertia for a long bar rotating around its centre
we obtain after substitutions,
= 24 kg × m2
b. In this case, we can take the wooden rod as a cylinder since its length is not much bigger than its radius. We have R = d / 2 = 12 cm / 2 = 6 cm = 0.06 m, h = 80 cm = 0.8 m and m = 400 g = 0.4 kg. Therefore, applying the equation
we obtain after substitutions,
= 0.02169 kg × m2
c. Moment of Inertia of a hollow sphere is calculated by the equation
where m = 600 g = 0.6 kg and R = 20 cm = 0.2 m. Substituting these values in the above equation, we obtain:
= 0.016 kg × m2
You have reached the end of Physics lesson 7.2.3 Moment of Inertia in Different Systems of Rotational Motion. There are 8 lessons in this physics tutorial covering Dynamics of Rotational Motion, you can access all the lessons from this tutorial below.
More Dynamics of Rotational Motion Lessons and Learning Resources
Whats next?
Enjoy the "Moment of Inertia in Different Systems of Rotational Motion" physics lesson? People who liked the "Dynamics of Rotational Motion lesson found the following resources useful:
- Different Systems Feedback. Helps other - Leave a rating for this different systems (see below)
- Rotation Physics tutorial: Dynamics of Rotational Motion. Read the Dynamics of Rotational Motion physics tutorial and build your physics knowledge of Rotation
- Rotation Revision Notes: Dynamics of Rotational Motion. Print the notes so you can revise the key points covered in the physics tutorial for Dynamics of Rotational Motion
- Rotation Practice Questions: Dynamics of Rotational Motion. Test and improve your knowledge of Dynamics of Rotational Motion with example questins and answers
- Check your calculations for Rotation questions with our excellent Rotation calculators which contain full equations and calculations clearly displayed line by line. See the Rotation Calculators by iCalculator™ below.
- Continuing learning rotation - read our next physics tutorial: Centripetal Force
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Dynamics of Rotational Motion" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.