Menu
Physics Lesson 7.2.8 - Power in Rotational Motion
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Power in Rotational Motion, this is the eighth lesson of our suite of physics lessons covering the topic of Dynamics of Rotational Motion, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Power in Rotational Motion
The last quantity in which the analogy between translational and rotational quantities is valid, is power. Thus, given that power in translational motion is
= F⃗ × ∆x⃗/t
= F⃗ × v⃗
we obtain for power in rotational motion
= τ × φ/t
= τ × ω
Example 5
The end of a 60 cm and 300 g rod start rotating from rest rotates in the horizontal plane through a small electric motor around a vertical axis as shown in the figure.
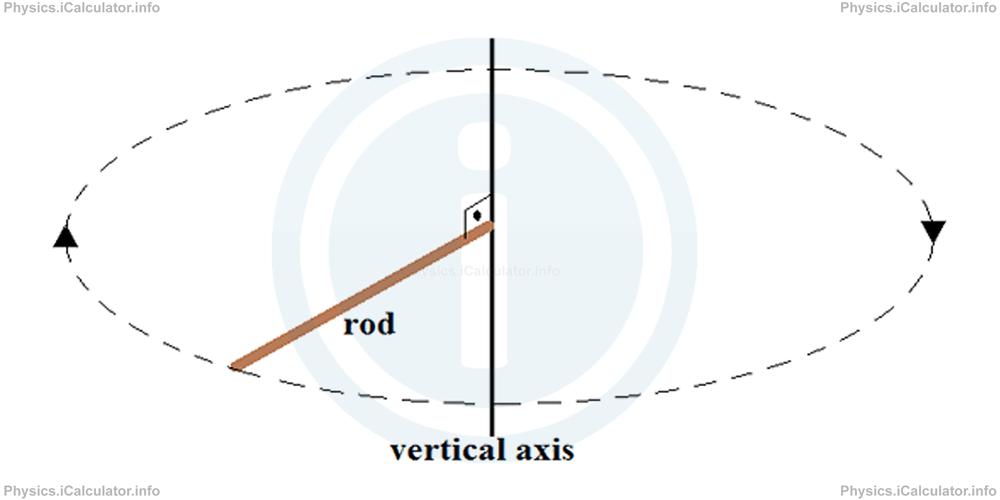
10 s after its start of rotation, the rod gains an angular velocity of 5 rad/s.
Calculate:
- Work done by the electric motor to rotate the rod
- Angular momentum at the end of 10 s
- Rotational kinetic energy of the rod at the end of 10 s
- Average power delivered by the motor supposing that all energy produced by it, is used to do work.
Solution 5
a. We must calculate torque and angle of rotation to find rotational work, as he Newton's Second Law of rotational motion is
Moment of inertia I of a bar rotating around its end is
where m = 300 g = 0.3 kg and L = 60 cm = 0.6 m. Thus,
= 0.036 kg × m2
Angular acceleration α is calculated by
where ω = 5 rad/s, ω0 = 0 and t = 10 s. Thus,
= 0.5 rad/s2
= 0.5 s-2
Hence,
= 0.036 kg × m2 × 0.5 s-2
= 0.018 kg × m2/s2
= 0.018 N × m
(Remember that 1 N = 1 kg × m/s2)
The angle φ wiped by the rod during its rotation is
= 0 × 10 + 0.5 × 102/2
= 25 rad
Hence, the rotational work done by the engine is
= 0.018 N × m × 25 rad
= 0.45 J
b. Angular momentum at the end of 10 s is
Substituting the values we found earlier, we obtain
= 0.18 kg × m2/s
c. Rotational kinetic energy of the rod at the end of 10 s is
= 0.036 kg × m2 × (5 rad/s)2/2
= 0.45 J
As you see, this value is equal to the work done by the motor to make the rod rotate.
d. Average power delivered by the motor supposing that all energy produced by it, is used to do work, is:
= 0.45 J/10 s
= 0.045 W
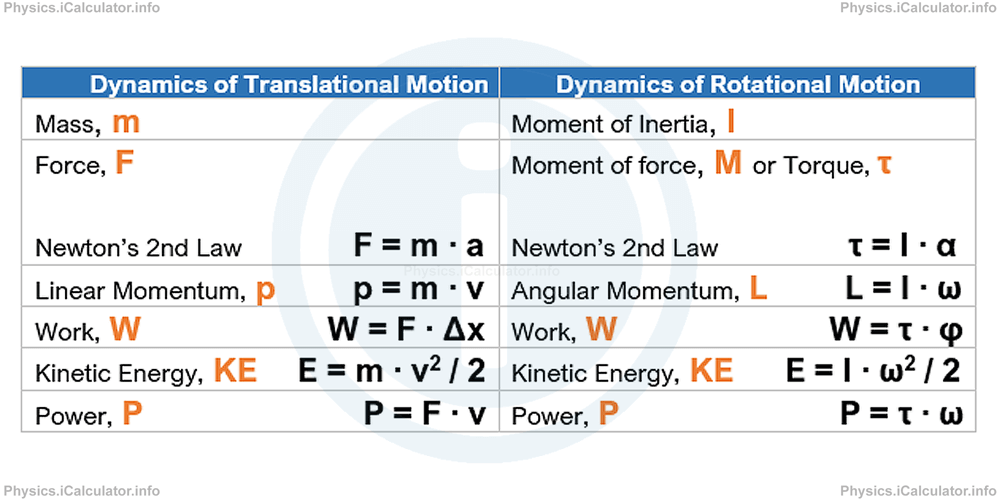
The following table includes everything discussed above regarding the relationship between dynamics translational and rotational quantities and the relevant formulae:
You have reached the end of Physics lesson 7.2.8 Power in Rotational Motion. There are 8 lessons in this physics tutorial covering Dynamics of Rotational Motion, you can access all the lessons from this tutorial below.
More Dynamics of Rotational Motion Lessons and Learning Resources
Whats next?
Enjoy the "Power in Rotational Motion" physics lesson? People who liked the "Dynamics of Rotational Motion lesson found the following resources useful:
- Power Feedback. Helps other - Leave a rating for this power (see below)
- Rotation Physics tutorial: Dynamics of Rotational Motion. Read the Dynamics of Rotational Motion physics tutorial and build your physics knowledge of Rotation
- Rotation Revision Notes: Dynamics of Rotational Motion. Print the notes so you can revise the key points covered in the physics tutorial for Dynamics of Rotational Motion
- Rotation Practice Questions: Dynamics of Rotational Motion. Test and improve your knowledge of Dynamics of Rotational Motion with example questins and answers
- Check your calculations for Rotation questions with our excellent Rotation calculators which contain full equations and calculations clearly displayed line by line. See the Rotation Calculators by iCalculator™ below.
- Continuing learning rotation - read our next physics tutorial: Centripetal Force
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Dynamics of Rotational Motion" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.