Menu
Kinematics of Rotational Motion
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
In addition to the revision notes for Kinematics of Rotational Motion on this page, you can also access the following Rotation learning resources for Kinematics of Rotational Motion
| Tutorial ID | Title | Tutorial | Video Tutorial | Revision Notes | Revision Questions | |
|---|---|---|---|---|---|---|
| 7.2 | Kinematics of Rotational Motion |
In these revision notes for Kinematics of Rotational Motion, we cover the following key points:
- The meaning of some quantities used as a background in the study of rotation, such as radius of curvature, period and frequency of rotation.
- Quantities involved in kinematics of uniform rotational motion, such as angular displacement and angular velocity.
- Quantities involved in kinematics of non-uniform rotational motion, such as angular acceleration and change in angular velocity.
- The relationship between linear and rotational quantities
- The meaning and formula of centripetal acceleration.
- Equations of all abovementioned quantities (there are more than one equation for each quantity)
Kinematics of Rotational Motion Revision Notes
A circular (rotational) motion involves the rotation of a particle about a fixed point in space by always keeping the same distance from this fixed point. Therefore, a rotational motion implies moving around a circle whose centre and radius are fixed.
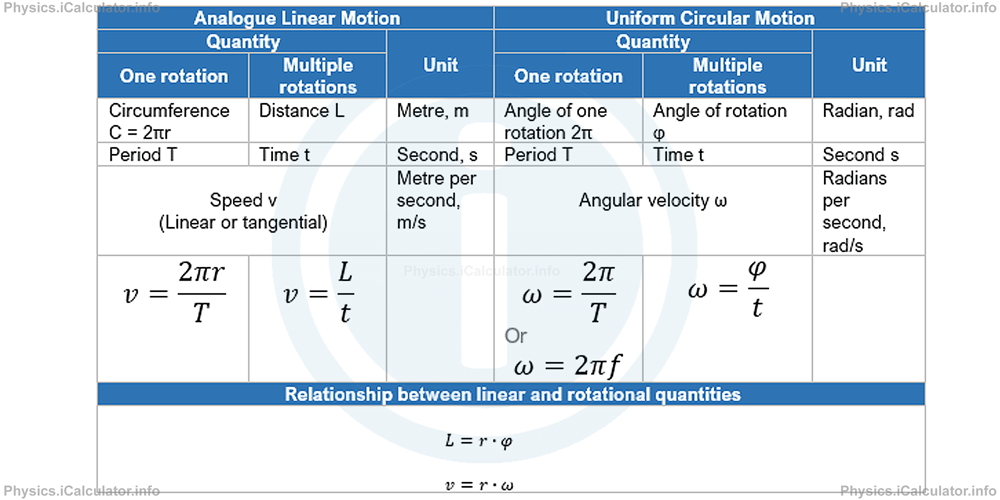
The time neccessary to make one complete revolution around a fixed point is called Period, T. It is measured by the unit of time, i.e. second, [s].
When an object rotates very fast around a fixed point, period results in a very small number. Therefore, to avoid the use of decimals, in such cases it is more suitable using the inverse of period, known as Frequency, f, to represent the time-related phenomena. Frequency is measured in revolutions per second, but this unit is widely recognized as Hertz [Hz] instead. Thus, we have
and
The simplest case of rotational motion is the uniform circular motion which represents objects moving at the same speed (not velocoty) around a fixed point by maintaining a constant distance from it. The reason why velocity is not constant although its magnitude doesn't change, is because the object's moving direction changes continously when it follows a circular path.
Angle of rotation, φ, is a very important parameter of rotational motion. This angle is measured in radians (rad) and it is also known as "angular displacement". When an object makes N rotations around a fixed point, the angle of rotation is
The arc length L represents the distance traveled by the object during its movement when the total angle is φ rad. Its relationship with the angular displacement is given by the formula
If we divide the angle of rotation by the time this process takes, we obtain another important quantity of rotational motion. It is known as the angular velocity, ω is measured in radians per second, [rad/s]. Its formula is
The table below gives the relationship between quantities in kinematics of both linear and rotational uniform motion.
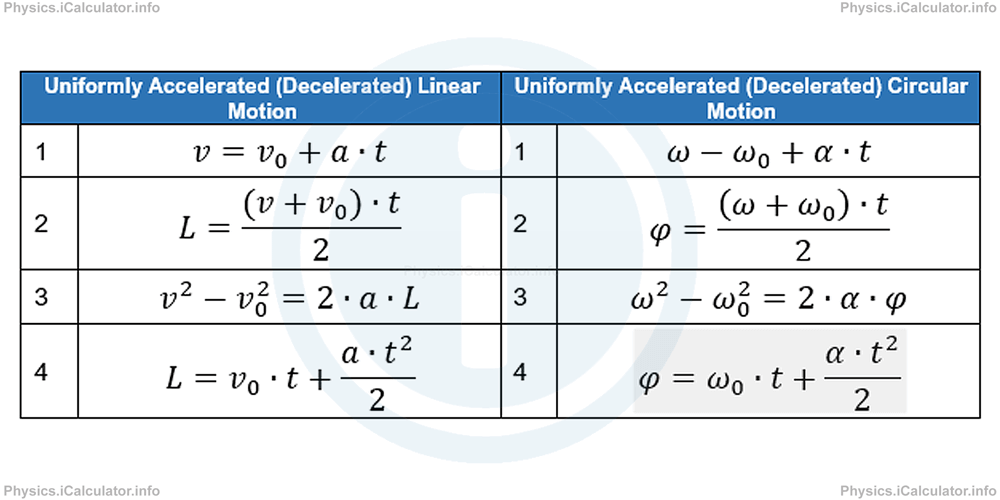
If the rotational motion is uniformly accelerated or decelerated, there is another quantity added. It is known as angular acceleration, α and is measured in [rad/s2].
Equations of uniformly accelerated or decelerated rotational motion and their relationship with those of uniformly accelerated or decelerated linear motion are shown in the table below.
In uniform rotational motion, the velocity is not the same everywhere despite its constant magnitude. This is because the velocity vector changes direction during the rotation. Therefore, we obtain a non-zero difference of velocity vectors which when divided by time gives a non-zero acceleration. Its vector always points towards the centre of curvature. That's why it is called centripetal acceleration, aC. Its formula is:
We calculate the magnitude of centripetal acceleration by the formula
The unit of centripetal acceleration is [m/s2] although it is an acceleration that occurs only in rotational motion. Therefore, centripetal acceleration acts as a bridge between linear and rotational quantities.
Whats next?
Enjoy the "Kinematics of Rotational Motion" revision notes? People who liked the "Kinematics of Rotational Motion" revision notes found the following resources useful:
- Revision Notes Feedback. Helps other - Leave a rating for this revision notes (see below)
- Rotation Physics tutorial: Kinematics of Rotational Motion. Read the Kinematics of Rotational Motion physics tutorial and build your physics knowledge of Rotation
- Rotation Practice Questions: Kinematics of Rotational Motion. Test and improve your knowledge of Kinematics of Rotational Motion with example questins and answers
- Check your calculations for Rotation questions with our excellent Rotation calculators which contain full equations and calculations clearly displayed line by line. See the Rotation Calculators by iCalculator™ below.
- Continuing learning rotation - read our next physics tutorial: Dynamics of Rotational Motion
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics tutorial "Kinematics of Rotational Motion" useful. If you did it would be great if you could spare the time to rate this physics tutorial (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.