Menu
Vector Product of Two Vectors
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
The following physics revision questions are provided in support of the physics tutorial on Vector Product of Two Vectors. In addition to this tutorial, we also provide revision notes, a video tutorial, revision questions on this page (which allow you to check your understanding of the topic) and calculators which provide full, step by step calculations for each of the formula in the Vector Product of Two Vectors tutorials. The Vector Product of Two Vectors calculators are particularly useful for ensuring your step-by-step calculations are correct as well as ensuring your final result is accurate.
Not sure on some or part of the Vector Product of Two Vectors questions? Review the tutorials and learning material for Vector Product of Two Vectors
| Tutorial ID | Title | Tutorial | Video Tutorial | Revision Notes | Revision Questions | |
|---|---|---|---|---|---|---|
| 2.5 | Vector Product of Two Vectors |
Cross (Vector) Product of Two Vectors Revision Questions
1. A force is acting at the given point in the beam shown in the figure.
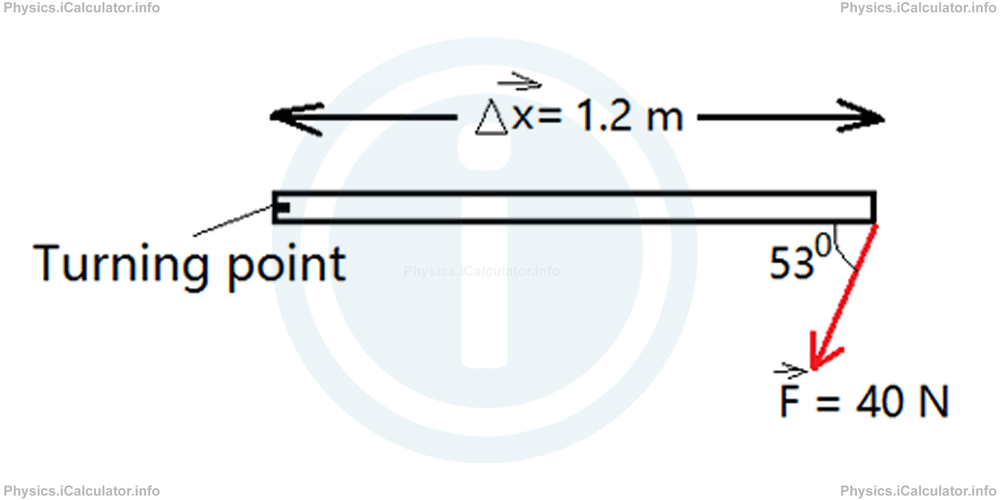
What is the magnitude of Moment of Force M⃗ taking place in the system? Moment of force is calculated by the equation M⃗ = F⃗ × ∆x⃗. Take cos 530 = 0.6 and sin 530 = 0.8.
- 48 N×m
- 40 N×m
- 38.4 N×m
- 28.8 N×m
Correct Answer: C
2. A 20 amps current carrying wire which is 40 cm long is placed at 300 to the magnetic field lines of induction b⃗ = 0.4 T. What is the magnetic force F⃗ acting in the wire? Take cos 300 = 0.86 and sin 300 = 0.5.
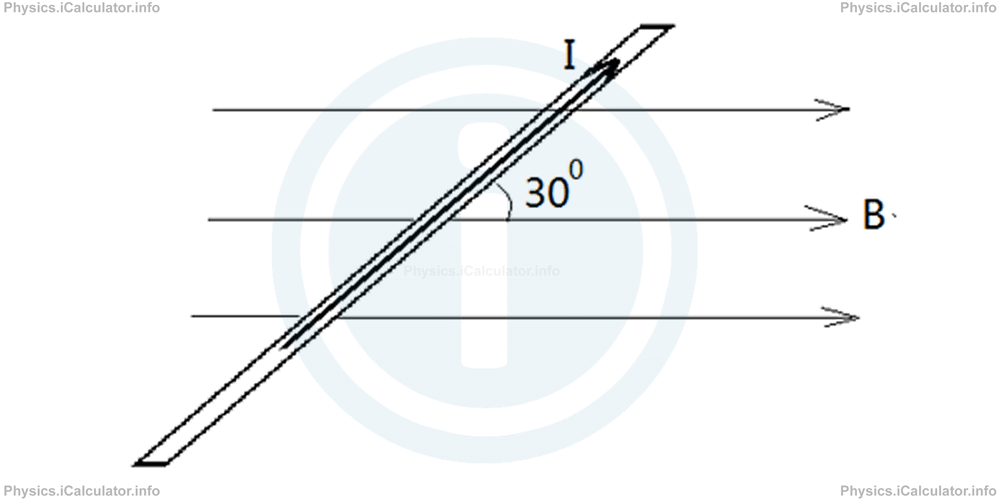
- 8 N
- 3.2 N
- 1.6 N
- 0.8 N
Correct Answer: C
3. Three forces are acting on the same object placed at the origin of the coordinates system. The tip of the first force is at (1, -3, 2) and that of the second force is at (4, 0, -1). What are the coordinates of the tip of the third force vector if these three forces obey the rule of vectors' cross production?
- (3, 9, 12)
- (-3, -9, -12)
- (4, 0, -2)
- (2, -2, 0)
Correct Answer: A
Whats next?
Enjoy the "Vector Product of Two Vectors" practice questions? People who liked the "Vector Product of Two Vectors" practice questions found the following resources useful:
- Practice Questions Feedback. Helps other - Leave a rating for this practice questions (see below)
- Vectors and Scalars Physics tutorial: Vector Product of Two Vectors. Read the Vector Product of Two Vectors physics tutorial and build your physics knowledge of Vectors and Scalars
- Vectors and Scalars Video tutorial: Vector Product of Two Vectors. Watch or listen to the Vector Product of Two Vectors video tutorial, a useful way to help you revise when travelling to and from school/college
- Vectors and Scalars Revision Notes: Vector Product of Two Vectors. Print the notes so you can revise the key points covered in the physics tutorial for Vector Product of Two Vectors
- Check your calculations for Vectors and Scalars questions with our excellent Vectors and Scalars calculators which contain full equations and calculations clearly displayed line by line. See the Vectors and Scalars Calculators by iCalculator™ below.
- Continuing learning vectors and scalars - read our next physics tutorial: Physics tutorials on Vectors In our next Physics tutorial, we explore Kinematics
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics tutorial "Vector Product of Two Vectors" useful. If you did it would be great if you could spare the time to rate this physics tutorial (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.