Menu
Physics Lesson 11.5.6 - Sound Level
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
Welcome to our Physics lesson on Sound Level, this is the sixth lesson of our suite of physics lessons covering the topic of Sound Waves. Intensity and Sound Level, you can find links to the other lessons within this tutorial and access additional physics learning resources below this lesson.
Sound Level
Sound Intensity does not vary linearly with power because distance is raised in power two in the formula that relates sound intensity and power. Therefore, it is not that easy dealing with it in calculations. Hence, scientists prefer to use another physical quantity known as sound level to describe the strength of sound waves. Sound level, L is measured in decibel (dB) in honour to Alexander Graham Bell and it is related to the sound intensity according a logarithmic scale, i.e.
where I is the intensity of the actual sound and I0 is the threshold of hearing. You may have read in the parameters plate of air conditioners or refrigerators the noise in dB these devices produce during their operation. (Noise level is another quantity measured in decibels as it represents irregular sound waves).
Since intensity of sound is the power per unit area, we can also use the equation
to represent the noise level. We can take the threshold sound power as P0 = 10 - 12 W.
Example 3
Sound power in heavy traffic is 0.001 W. What is the value of noise level in dB caused by the heavy traffic?
Solution 3
We have P = 0.001 W = 10 - 3 W and P0 = 10 - 12 W. Thus,
= 10 × log(10-3/10-12))
= 10 × log10-3-(-12)
= 10 × log109
= 9 × 10
= 90 dB
(Here the logarithm properties log ab = b × log a and log 10 = 1 are used).
The advantage of using a logarithmic scale for calculating the sound level consists on the small range of sound level values when intensity changes too much. Let's consider an example to illustrate this point.
Example 4
A machinery in a factory produces a sound of intensity equal to 100 dB. What is the sound level produced by 40 such machineries if they are turned on simultaneously?
Solution 4
The procedure to solve this problem is as follows: We must calculate the sound intensity produced by a single machinery first, and then multiply it by 40. Then we must calculate the new sound level in dB. Thus,
100 = 10 × log(I1/10-12)
100/10 = log I1 - log10-12
10 = log I1 - (-12) × log10
10 = log I1 + 12 × 1
log I1 = -2
I1 = 10 - 2
= 0.01 W/m2
The sound intensity produced by 40 such machineries therefore is
= 40 × 0.01 W/m2
= 0.4 W/m2
= 4 × 10-1 W/m2
Hence, the sound level produced by these 40 machineries when they turn on simultaneously is
= 10 × log(4 × 10-1/10-12 )
= 10 × log4 × 1011
= 10 × (log 4 + log1011)
= 10 × (log 4 + 11 × log10)
= 10 × (0.6 + 11)
= 10 × 11.6
= 116 dB
You may notice that for a 40 times increase in sound intensity, the sound level increases only by 16 dB (from 100 dB to 116 dB). Therefore, don't neglect the slight changes in the values of sound level as they represent a very big change in sound intensity.
Below some typical values for sound intensity and sound level are given.
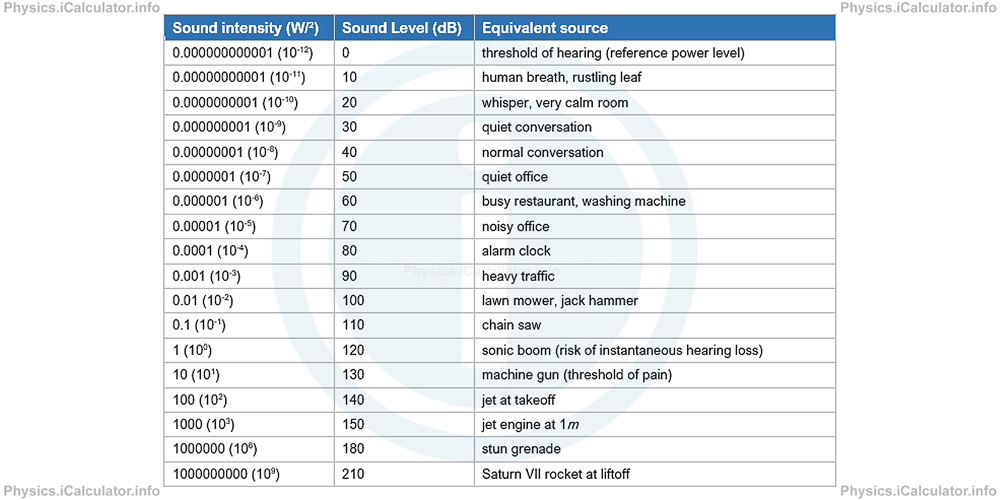
You have reached the end of Physics lesson 11.5.6 Sound Level. There are 7 lessons in this physics tutorial covering Sound Waves. Intensity and Sound Level, you can access all the lessons from this tutorial below.
More Sound Waves. Intensity and Sound Level Lessons and Learning Resources
Whats next?
Enjoy the "Sound Level" physics lesson? People who liked the "Sound Waves. Intensity and Sound Level lesson found the following resources useful:
- Level Feedback. Helps other - Leave a rating for this level (see below)
- Waves Physics tutorial: Sound Waves. Intensity and Sound Level. Read the Sound Waves. Intensity and Sound Level physics tutorial and build your physics knowledge of Waves
- Waves Revision Notes: Sound Waves. Intensity and Sound Level. Print the notes so you can revise the key points covered in the physics tutorial for Sound Waves. Intensity and Sound Level
- Waves Practice Questions: Sound Waves. Intensity and Sound Level. Test and improve your knowledge of Sound Waves. Intensity and Sound Level with example questins and answers
- Check your calculations for Waves questions with our excellent Waves calculators which contain full equations and calculations clearly displayed line by line. See the Waves Calculators by iCalculator™ below.
- Continuing learning waves - read our next physics tutorial: Electromagnetic Waves. Light
Help others Learning Physics just like you
Please provide a rating, it takes seconds and helps us to keep this resource free for all to use
We hope you found this Physics lesson "Sound Waves. Intensity and Sound Level" useful. If you did it would be great if you could spare the time to rate this physics lesson (simply click on the number of stars that match your assessment of this physics learning aide) and/or share on social media, this helps us identify popular tutorials and calculators and expand our free learning resources to support our users around the world have free access to expand their knowledge of physics and other disciplines.